Миллиарды и миллиарды: Размышления о жизни и смерти на рубеже тысячелетий

Переводчик Наталья Киеченко

Редактор Вячеслав Ионов

Научный редактор Владимир Сурдин, канд. физ. – мат. наук

Руководитель проекта И. Серёгина

Корректоры М. Миловидова, Е. Аксёнова

Компьютерная верстка А. Фоминов

Дизайнер обложки Ю. Буга

© 1997 by The Estate of Carl Sagan with permission from Democritus Properties, LLC.

© Издание на русском языке, перевод, оформление. ООО «Альпина нон-фикшн», 2017

Все права защищены. Произведение предназначено исключительно для частного использования. Никакая часть электронного экземпляра данной книги не может быть воспроизведена в какой бы то ни было форме и какими бы то ни было средствами, включая размещение в сети Интернет и в корпоративных сетях, для публичного или коллективного использования без письменного разрешения владельца авторских прав. За нарушение авторских прав законодательством предусмотрена выплата компенсации правообладателя в размере до 5 млн. рублей (ст. 49 ЗОАП), а также уголовная ответственность в виде лишения свободы на срок до 6 лет (ст. 146 УК РФ).

* * *

Моей сестре Кэри, одной из шести миллиардов

Часть I
Наглядность и красота чисел

Глава 1
Миллиарды и миллиарды

Есть люди, думающие, что число песчинок бесконечно. …Другие думают, что хотя число это и не бесконечно, но большего представить себе невозможно. …Я, напротив, постараюсь доказать с геометрической точностью, которая убедит тебя, что… есть числа, превышающие число песчинок, которые можно вместить не только в пространстве, равном объему земли… но и целого мира.

– Архимед (ок. 287–212 гг. до н. э.). Исчисление песчинок^[1]

Клянусь, фразы «миллиарды и миллиарды» я не говорил! Мог сказать, например, «100 миллиардов галактик и 10 миллиардов триллионов звезд». Невозможно описывать космос, не прибегая к большим числам. Я неоднократно произносил слово «миллиард» в программах телевизионного цикла «Космос», которые смотрело великое множество зрителей. Но «миллиарды и миллиарды» – ни разу. Хотя бы потому, что это слишком неопределенно. «Миллиарды и миллиарды» – это сколько? Два-три миллиарда? Двадцать? Сто? Разброс слишком велик. При подготовке новой редакции цикла телепередач я все внимательно пересмотрел и убедился, что ничего подобного не говорил.

Эту фразу сказал Джонни Карсон, гостем которого в «Вечернем шоу» я успел побывать уже не менее трех десятков раз. Он обряжается в вельветовый пиджак и водолазку, взлохмачивает волосы и, пародируя меня, эдакий двойник, запускает что-нибудь вроде «миллиардов и миллиардов» в вечерний телеэфир. И мне начинает надоедать, что эта пародия живет собственной жизнью, изрекая сентенции, которыми друзья и коллеги ошарашивают меня на следующее утро. (В остальном признаю, что серьезный астроном-любитель Карсон чаще всего говорит на строгом научном языке.)

Увы, «миллиарды и миллиарды» прижились. Людям нравится, как это звучит. Меня то и дело окликают на улице, в самолете, на вечеринке и с легким смущением просят оказать любезность и произнести: «Миллиарды и миллиарды».

– Видите ли, это не мои слова, – объясняю я.

– Ну и ладно, – отвечают мне. – Все равно скажите.

Оказывается, Шерлок Холмс никогда не говорил «элементарно, Ватсон» (по крайней мере в книгах Артура Конана Дойла), Джимми Кэгни^[2] не изрекал «ты грязная крыса», а герой Хамфри Богарта^[3] не произносил «сыграй это еще раз, Сэм». Но эти фразы настолько прочно укоренились в популярной культуре, что воспринимаются как действительно сказанные.

Вот и не слишком удачное выражение про миллиарды по-прежнему приписывают мне в компьютерных журналах («Карл Саган сказал бы, что для этого нужны миллиарды и миллиарды байтов»), в экономических обзорах на страницах газет, в рассказах о гонорарах спортивных звезд и т. д.

В былое время я бы ни за что не повторил такого ни устно, ни письменно – из вредности. Но теперь я это перерос. И если так надо для истории, пожалуйста:

– Миллиарды и миллиарды!

Почему эта фраза стала настолько популярной? Когда-то символом больших чисел выступал «миллион». Супербогатеи были миллионерами. Население Земли во времена Иисуса составляло около 250 млн человек. Конвент 1787 г. дал Конституцию четырем миллионам американцев; к началу Второй мировой войны нас было уже 132 млн. От Земли до Солнца 150 млн км. В Первую мировую погибли около 40 млн человек, во Вторую – 60 млн. В году 31,7 млн секунд (можете проверить). Совокупной мощи ядерных арсеналов, накопленных к концу 1980-х гг., хватило бы, чтобы уничтожить миллион Хиросим. Долгое время в большинстве случаев слово «миллион», в сущности, означало «неимоверно много».

Но времена изменились. Ныне в мире есть прослойка миллиардеров, и вовсе не потому, что деньги обесценились. Возраст Земли, по общему признанию, составляет 4,6 млрд лет. Численность населения давно превысила 6 млрд. Два ваших дня рождения разделяет один год и миллиард километров (Земля движется вокруг Солнца гораздо быстрее, чем удаляются от нее запущенные в космос «Вояджеры»). Четыре бомбардировщика В-2 стоят миллиард долларов (по другим расчетам два и даже четыре миллиарда). Годовой оборонный бюджет США с учетом всех скрытых расходов превышает $300 млрд. В случае полномасштабной ядерной войны между США и Россией сразу же погибнут около миллиарда человек. Несколько сантиметров вещества – это цепочка из миллиарда атомов. Звезды и галактики также исчисляются многими миллиардами.

В 1980 г., когда начался телевизионный показ цикла «Космос», люди были готовы считать миллиардами. Миллионов уже не хватало, они не поражали воображения. Между тем эти два слова звучат похоже, их нетрудно перепутать. Поэтому в эфире «Космоса» я произносил «миллиард» с такой подчеркнутой артикуляцией, что многие зрители сочли это акцентом или дефектом речи.

Вспоминается старая шутка. Лектор планетария рассказывает посетителям, что через 5 млрд лет Солнце превратится в красный гигант и поглотит Меркурий и Венеру, а в конечном счете, возможно, и Землю. После лекции в него вцепляется встревоженный слушатель:

– Простите, как вы сказали? Солнце сожжет Землю через пять миллиардов лет?

– Да, приблизительно.

– Слава богу! Мне было послышалось «пять миллионов».

Будь то пять миллионов или пять миллиардов лет, будущая кончина Земли представляет для нас чисто теоретический интерес. Но, когда дело касается государственных бюджетов, населения планеты или числа жертв ядерной войны, разница между этими величинами имеет очень большое значение.

Фраза «миллиарды и миллиарды» пока не утратила популярности, но и ей уже недостает размаха. Не за горами новый эталон большого числа – триллион.

Мировые военные расходы уже достигают $1 трлн в год. Совокупный долг развивающихся стран западным банкам приближается к $2 трлн (по сравнению с $60 млрд в 1970 г.). Годовой бюджет правительства США также недалек от $2 трлн. Государственный долг – около $5 трлн. Расходы на технически сомнительную затею рейгановской эпохи, Стратегическую оборонную инициативу, оценивались в $1–$2 трлн. Все растения Земли весят триллион тонн. В масштабах космоса триллионами измеряется буквально всё. От Солнечной системы до ближайшей звезды, альфа Кентавра, около 40 трлн км.

В повседневной жизни люди традиционно путают миллионы, миллиарды и триллионы, и не проходит недели без подобной ошибки в теленовостях (чаще всего «страдают» миллион и миллиард). Поэтому позвольте мне лишний раз напомнить: миллион (million по-английски) – это тысяча тысяч, или единица с шестью нулями; миллиард (billion) – тысяча миллионов, единица с девятью нулями; триллион (trillion) – тысяча миллиардов (или, это то же самое, миллион миллионов), что записывается как единица с 12 нулями.

Так принято в Америке. Долгое время в британском английском словом billion обозначалось число, которое в Америке называют триллионом, а американский billion англичане – вполне обоснованно – именовали «тысячей миллионов». В Европе миллиард обозначался словом milliard. Я с детства коллекционирую почтовые марки, и у меня есть непогашенная марка, выпущенная в Германии в 1923 г., в самый разгар инфляции, с надписью «50 миллиардов». Отправить письмо стоило 50 триллионов немецких марок. (В те времена в булочную или бакалею ходили с тачкой, полной наличности.) Ныне в силу большого влияния США на мир слово milliard во многих странах вышло из употребления.

Самый надежный способ понять, о каком числе идет речь, очень прост – сосчитать нули после единицы. Правда, если нулей очень много, дело это канительное. Поэтому группы по три нуля разделяют при записи запятыми или пробелами. Например, триллион выглядит как 1,000,000,000,000 или 1 000 000 000 000. (В Европе вместо запятых ставятся точки.) Сталкиваясь с числами больше триллиона, вы должны каждый раз считать, сколько раз по три нуля в них содержится. Было бы гораздо удобнее, называя число, сразу говорить, сколько в нем нулей после единицы.

Ученые и математики, люди практичные, так и поступают – пользуются так называемым экспоненциальным представлением. Пишется число десять, к которому вверху справа приписывается мелким шрифтом показатель – число, соответствующее количеству знаков после единицы. Таким образом, 10⁶ = 1 000 000, 10⁹ = 1 000 000 000, 10¹² = 1 000 000 000 000 и т. д. Этот показатель называется экспонентом, степенью или порядком числа. Например, 10⁹ читается как «десять в девятой степени» (исключение составляют 10² и 10³, которые принято называть «десять в квадрате» и «десять в кубе»). Понятие степени или порядка – наряду с некоторыми другими терминами из естественных наук и математики, например «параметр», – проникает в повседневный язык, но его смысл все более размывается.

Помимо наглядности у экспоненциального представления чисел есть замечательное дополнительное преимущество – возможность перемножать любые два числа простым сложением их степеней. Скажем, 1000 × 1 000 000 000 = 10³ × 10⁹ = 10¹². Или возьмем числа побольше: в средней галактике 10¹¹ звезд, самих галактик тоже 10¹¹, следовательно, в космосе около 10²² звезд.

Тем не менее экспоненциальное представление встречают в штыки люди, у которых не ладится с математикой (хотя оно, наоборот, проще для понимания), и наборщики, которых хлебом не корми – дай набрать 109 вместо 10⁹ (сотрудники издательства Random House, как видите, являются счастливым исключением).

Первые шесть больших чисел, имеющих названия, приводятся далее во врезке. Каждое число в 1000 раз больше предыдущего. Названия чисел больше триллиона практически не употребляются. Если считать круглые сутки без остановки, прибавляя по единице в секунду, потребуется больше недели, чтобы досчитать до миллиона. На миллиард у вас уйдет полжизни. До квинтиллиона вы не доберетесь, даже если проживете столько, сколько существует Вселенная.

Овладев экспоненциальным представлением, вы с легкостью справитесь с непостижимо большими числами, такими как примерное количество микробов в чайной ложке почвы (10⁸), песчинок на всех земных пляжах (порядка 10²⁰), живых существ на нашей планете (10²⁹), атомов во всем живом на Земле (10⁴¹), атомных ядер в Солнце (10⁵⁷) или элементарных частиц (электронов, протонов, нейтронов) во всем космосе (10⁸⁰). Вы все равно не сможете представить миллиард или квинтиллион объектов – и никто не сможет. Но благодаря экспоненциальному представлению мы в состоянии оперировать подобными величинами и использовать их в расчетах. Неплохо для самоучек, которые явились в этот мир ни с чем и пересчитывали соплеменников по пальцам рук и ног!

Названия еще более крупных чисел: секстиллион (10²¹), септиллион (10²⁴), октиллион (10²⁷), нониллион (10³⁰) и дециллион (10³³). Масса Земли 6 октиллионов грамм.

Помимо принятого в науке экспоненциального представления каждое число можно выразить и словами с помощью приставок. Например, электрон имеет один фемтометр (10^–15 м) в поперечнике, длина волны желтого света – полмикрометра (0,5 мкм), глаз человека способен различить насекомое размером в одну десятую миллиметра (10^–4 м), радиус Земли 6300 км (6,3 мегаметра), вес средней горы 100 петаграмм (10¹⁷ г). Вот все возможные приставки и их значения:

По-настоящему большие числа – кровь и плоть современной науки, но не следует думать, что это сегодняшнее изобретение.

В Индии арифметика давно овладела громадными числами. В индийских газетах часто можно прочитать о расходах в лакхах или крорах рупий. Система выглядит следующим образом: дас – 10, сан – 100, хазар – 1000, лакх – 10⁵, крор – 10⁷, арахб – 10⁹, карахб – 10¹¹, ниэ – 10¹³, падхам – 10¹⁵ и санкх – 10¹⁷. Жившие на территории современной Мексики индейцы майя, цивилизацию которых уничтожили пришельцы из Европы, составили календарь, перед протяженностью которого меркнут жалкие несколько тысяч лет, миновавших, по мнению европейцев, от сотворения мира. Среди руин города Коба в мексиканском штате Кинтана-Роо обнаружены надписи, согласно которым майя оценивали возраст Вселенной примерно в 10²⁹ лет. Индуисты полагали, что нынешнему воплощению Вселенной 8,6 × 10⁹ лет, – и попали почти в точку. А математик Архимед, живший на Сицилии в III в. до н. э., в своей книге «Исчисление песчинок» рассчитал, что для заполнения всего космоса необходимо 10⁶³ крупиц песка. Уже в те времена миллиардов и миллиардов явно не хватало, чтобы решать по-настоящему масштабные задачи.

Глава 2
Персидские шахматы

Не может быть языка более всеобъемлющего, чем аналитические уравнения, и более простого, лишенного ошибок и неясностей, т. е. более достойного для выражения неизменных соотношений реального мира… Математический анализ, являясь способностью человеческого разума, восполняет краткость нашей жизни и несовершенство наших чувств.

– Жан Батист Жозеф Фурье. Аналитическая теория тепла (1822 г.)^[4]

В известном мне варианте эта история произошла в Древней Персии, хотя с тем же успехом могла случиться в Индии и даже в Китае. В любом случае это было давным-давно. Великий визирь, главный советник правителя, изобрел новую игру, в которой следовало передвигать фигуры по квадратной доске, расчерченной на 64 клетки красного и черного цвета. Самой главной фигурой был правитель, следующей по значимости – визирь, как и следовало ожидать, учитывая личность изобретателя. Цель игрока состояла в том, чтобы уничтожить главную фигуру противника, и по соответствующим словам персидского языка (шах – правитель, мат – смерть) игра получила название «шахматы». Буквально, «смерть правителя». В русском языке эта игра так до сих пор и называется, в чем, видимо, сказывается особая революционность русского народа. Время шло, менялись фигуры, их ходы и правила игры. Так, место визиря теперь занимает ферзь, обладающий несравнимо большими возможностями.

Как шаху могла понравиться игра «Убей правителя» – загадка. Однако, гласит легенда, шах был настолько восхищен новым развлечением, что предложил великому визирю самому назначить себе награду. Предложение не застало того врасплох. Визирь ответил, что он человек скромный и просьба его будет самой скромной. Вот игровая доска, расчерченная на восемь столбцов и восемь рядов. Пусть на первую клетку положат всего лишь одно зернышко пшеницы, на вторую в два раза больше, на третью – еще в два раза больше и так далее, пока все клетки не будут заполнены. Шах запротестовал. Столь ничтожная плата за такое замечательное изобретение! Он предлагал драгоценности, красавиц, дворцы. Но мудрец, смиренно потупившись, отвергал любые дары. Все, что ему нужно, – малая толика пшеницы. И правитель, втайне сетуя на непритязательность и упрямство своего советника, согласился.

Однако, когда хранитель царской житницы принялся отсчитывать зерно, открылся неприятный сюрприз. Все началось с малого: 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024… Но чем дальше, тем более чудовищными, невообразимо огромными становились числа. Последней, 64-й клетке соответствует почти 18,5 квинтиллиона (см. врезку далее). Вероятно, великий визирь сидел на диете с высоким содержанием клетчатки.

Сколько весят 18,5 квинтиллиона зерен пшеницы? Если принять размер каждого зернышка равным миллиметру, то их общий вес составит около 75 млрд тонн – намного больше запасов любого шаха. Собственно говоря, это урожай за 150 лет при современных объемах производства. Дальнейшее тонет во мраке времен. Уступил ли шах мудрецу свою державу, коря себя за пренебрежение арифметикой, или предпочел сыграть в новую игру «визирьмат», осталось неведомым.

Возможно, история изобретения персидских шахмат – всего лишь сказка. Но древние персы и индийцы действительно совершили немало блистательных открытий в математике и хорошо представляли, какие результаты дает последовательное удвоение. Если бы шахматные партии разыгрывались на доске с сотней клеток (10 × 10), шах задолжал бы визирю пшеницу общим весом, равным весу Земли. Числовая последовательность, в которой каждое следующее число является результатом умножения предыдущего на фиксированную величину, называется геометрической прогрессией, а соответствующий процесс увеличения итога – экспоненциальным ростом.

Геометрические прогрессии встречаются во всех важных сферах жизни, обыденных и экзотических. Для примера рассмотрим сложный процент. Если бы ваш предок 200 лет назад, вскоре после Войны за независимость, положил в банк $10 под 5 % годовых, то на счете уже было бы $10 × 1,05²⁰⁰, или $172 925,81. (Чтобы узнать, сколько будет 1,05²⁰⁰, нужно попросту умножить число 1,05 само на себя 200 раз.) Жаль, что немногие предки так заботятся о благосостоянии отдаленных потомков, да и $10 – в те времена солидная сумма – нашлись бы не у каждого. Если бы ваш щедрый пращур разместил вклад под 6 % годовых, вы бы унаследовали больше миллиона, под 7 % – больше $7,5 млн. Фантастические 10 % годовых принесли бы вам кругленькую сумму – $1,9 млрд.

Аналогично «работает» инфляция. При уровне инфляции 5 % в год доллар через год будет стоить $0,95, через два года (0,95)² = $0,91, через 10 лет «похудеет» до $0,61, через 20 – до $0,37 и т. д. Это самым непосредственным образом касается пенсионеров, годовые выплаты которым являются фиксированными и не индексируются с учетом инфляции.

Многократное удвоение и, следовательно, экспоненциальный рост – характерная особенность воспроизводства биологических организмов. Начнем с простого примера – бактерии, размножающейся делением. Через положенное время каждая из двух дочерних бактерий также делится надвое. При достаточном количестве пищи и отсутствии ядов в среде обитания колония бактерий растет в геометрической прогрессии. В самых благоприятных условиях удвоение их численности происходит примерно каждые 15 минут: четыре удвоения в час, 96 в сутки. Одна бактерия весит около одной триллионной доли грамма, но всего через сутки безудержного размножения ее потомки сравняются весом с горой, через каких-нибудь полтора дня – с Землей, а через двое суток перетянут на весах Солнце… Пройдет еще немного времени, и вся Вселенная будет заполнена бактериями. Перспективы не слишком радужные, но, к счастью, несбыточные. Почему? Потому что подобный экспоненциальный рост неизбежно упирается в тот или иной естественный барьер. Букашки, например, съедают всю пищу, отравляют друг друга или перестают спариваться, когда их слишком много. Экспоненциальный рост не может продолжаться вечно, иначе он поглотил бы все, но задолго до этого в игру вступает сдерживающий фактор. Экспоненциальная кривая выходит на плато (см. рисунок).

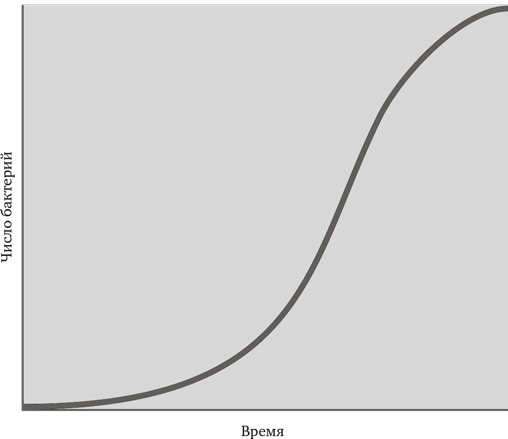
Эта особенность очень важна в свете эпидемии СПИДа. Ныне во многих странах количество людей с симптомами этой болезни растет в геометрической прогрессии, удваиваясь ежегодно. Это значит, что каждый год носителей вируса СПИД становится в два раза больше, чем было в прошлом году. СПИД уже привел к огромным людским потерям. Если бы экспоненциальное распространение эпидемии продолжилось, человечество ждала бы небывалая катастрофа. Через 10 лет число заболевших увеличилось бы в тысячу раз, а через 20 лет – в миллион. Умножив нынешнее количество больных на миллион, получим результат, намного превышающий население Земли. Если бы ежегодное удвоение числа больных СПИДом не имело никаких естественных ограничений, а само заболевание неизбежно приводило к фатальному исходу (и было абсолютно неизлечимым), то все земляне умерли бы от СПИДа, и очень быстро.

Однако некоторые люди обладают врожденным иммунитетом. Кроме того, по данным Центра по борьбе с инфекционными болезнями Министерства здравоохранения США, экспоненциальный рост заболеваемости СПИДом поначалу происходил почти исключительно в группах риска, представители которых – прежде всего гомосексуальные мужчины, больные гемофилией и лица, употребляющие внутривенные наркотики, – практически не имеют половых контактов с остальным населением. Если лекарство от СПИДа не будет найдено, героиновые наркоманы, имеющие привычку колоться общими иглами, умрут. Не все – благодаря врожденному иммунитету, но почти все. Та же судьба ждет гомосексуалистов, имеющих беспорядочные и незащищенные связи, однако минует тех, кто никогда не пренебрегает средствами защиты, хранит верность постоянному партнеру, а также входит в число немногих счастливчиков, невосприимчивых к этому заболеванию. Стопроцентные гетеросексуалы, с начала 1980-х гг. не изменяющие друг другу (или практикующие безопасный секс), при условии, что они не пользуются общими шприцами, – а таких людей большинство – в общем, застрахованы от СПИДа. После того как кривые заболеваемости групп наибольшего риска выйдут на плато, настанет очередь менее уязвимых групп. В настоящее время в Америке это, видимо, гетеросексуальная молодежь, не умеющая обуздывать страсти и увлекающаяся небезопасными экспериментами. Многие из них умрут, кого-то спасет везение, врожденный иммунитет или воздержанность, а пик роста заболеваемости переместится в очередную по рискованности группу – возможно, следующее поколение мужчин-гомосексуалистов. В итоге экспоненциальная кривая всего человечества выйдет на плато, а СПИД убьет гораздо меньше людей, чем все население Земли (что, впрочем, едва ли утешит множество его жертв и их близких).

* * *

Кризис перенаселения Земли также связан с явлением экспоненциального роста. Большую часть существования человечества его численность была практически постоянна – рождаемость и смертность уравновешивали друг друга. Такое состояние называется динамическим равновесием. С развитием сельского хозяйства, включая методы возделывания той самой пшеницы, которую так жаждал великий визирь, численность людей стала увеличиваться и вошла в фазу экспоненциального роста. А это что угодно, только не равновесие. Сейчас население нашей планеты удваивается за 40 лет. Каждые 40 лет нас становится в два раза больше. Английский священник Томас Мальтус еще в 1798 г. заметил: население, растущее по экспоненте, – в терминологии Мальтуса, в геометрической прогрессии – будет голодать при любом росте производства продуктов питания. Никакая зеленая революция, никакая гидропоника, никакое освоение пустынь не компенсирует экспоненциального роста количества едоков.

За пределами Земли решения этой проблемы также не существует. Сейчас ежедневно рождается примерно на 240 000 человек больше, чем умирает. Наши возможности, мягко говоря, недостаточны, чтобы отправлять в космос 240 000 переселенцев в день. Никакие базы на земной орбите, на Луне или на Марсе не вместят сколько-нибудь заметную часть столь бурно растущего населения. Даже если бы мы могли перебросить всех в другие звездные системы на кораблях со сверхсветовыми скоростями, это бы не помогло. Все пригодные для жизни планеты Млечного Пути оказались бы перенаселенными уже через тысячелетие. Все бесполезно, пока мы не снизим темпы воспроизводства. Экспоненциальный рост – это серьезно.

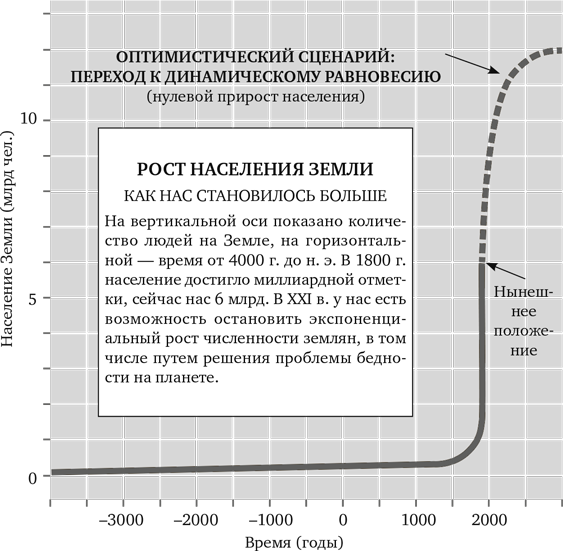
На рисунке ниже представлена кривая изменения населения Земли. Сейчас мы находимся как раз в фазе резкого экспоненциального роста (или вот-вот из нее выйдем). Но многие страны, например США, Россия и Китай, уже достигли или скоро достигнут состояния, в котором рост населения тормозится и наступает динамическое равновесие. Это так называемый нулевой прирост популяции. Однако рост в геометрической прогрессии настолько масштабен, что общая ситуация все равно не изменится, если хотя бы малая часть землян будет и дальше воспроизводиться экспоненциально. Общая численность человечества также будет расти экспоненциально.

Существует убедительно доказанная связь бедности и высокой рождаемости. В странах больших и малых, капиталистических и коммунистических, католических и мусульманских, на Западе и на Востоке – практически везде экспоненциальный прирост населения замедляется или прекращается, когда удается победить нищету. Происходит так называемый демографический сдвиг. Насущнейшая стратегическая необходимость человеческого вида – реализовать этот сдвиг во всех уголках нашей планеты. Не только в силу морального долга, но и с точки зрения прямой выгоды богатые страны должны помочь бедным добиться экономической стабильности. Одна из главных причин мирового демографического кризиса – бедность.

У демографического сдвига имеются любопытные исключения. Есть страны, где при высоком среднедушевом доходе уровень рождаемости все равно значителен. Это государства, где населению практически не доступны средства контрацепции и/или женщины практически лишены политического влияния. Связь между этими факторами очевидна.

Во время работы над этой книгой на Земле жило около 6 млрд человек. При сохранении нынешних темпов роста через 40 лет нас будет 12 млрд, через 80 лет – 24 млрд, через 120 лет – 48 млрд… По общему мнению, Земля не способна прокормить столько людей. Нас уже настолько много, что искоренение бедности в мировом масштабе представляется самым дешевым и, разумеется, самым гуманным способом преодоления кризиса из всех, которыми человечество будет располагать еще многие десятилетия. Наша задача – обеспечить повсеместный демографический сдвиг и вывести на плато кривую роста населения. Мы должны избавить жителей всех стран от нищеты, обеспечить их безопасными и эффективными средствами контроля рождаемости и сделать женщин реальной силой в обществе (путем допуска в исполнительные, законодательные, судебные органы власти, силовые ведомства и институты, влияющие на общественное мнение). В противном случае активизируются другие процессы, над которыми мы не властны.

* * *

Кстати говоря…

Идея деления атомного ядра впервые пришла в голову венгерскому физику-эмигранту Лео Сциларду в Лондоне в сентябре 1933 г. Его занимал вопрос о том, дано ли человеку высвободить колоссальную энергию, заключенную в ядре атома. Что произойдет, если направить нейтрон в ядро? (Из-за отсутствия электрического заряда нейтрон не будет отталкиваться положительно заряженными протонами и столкнется с ядром.) Пока ученый ждал зеленого сигнала светофора на перекрестке Саутгемптон-роу, его осенило, что может существовать некое вещество, какой-то химический элемент, атом которого при соударении с одним нейтроном испускает два! Каждый из этих двух нейтронов может выбить еще по паре нейтронов из других атомов… И перед мысленным взором Сциларда предстала картина цепной ядерной реакции – лавинообразный процесс экспоненциального размножения нейтронов и распада атомных ядер. Тем вечером в маленьком номере отеля Strand Palace он рассчитал, что лишь несколько килограммов вещества, если бы удалось вызывать в нем управляемую цепную реакцию, могли бы целый год снабжать энергией небольшой город… Или мгновенно уничтожить этот город, если бы вся эта энергия выделилась одномоментно. Впоследствии Сцилард эмигрировал в США и начал методично перебирать химические элементы в поисках такого, атомы которого при бомбардировке нейтронами излучают больше нейтронов, чем с ними сталкивается. Уран показался ему многообещающим. Сцилард убедил Альберта Эйнштейна написать ставшее знаменитым письмо президенту Рузвельту с призывом как можно скорее создать в США атомную бомбу. Сцилард возглавил первый успешный эксперимент по делению урановых ядер, поставленный в Чикаго в 1942 г., который и стал первым шагом на пути к созданию ядерного оружия, и всю оставшуюся жизнь пытался раскрыть человечеству глаза на опасность чудовищной силы, которую сам же выпустил на свободу. Так Лео Сцилард открыл для себя мощь экспоненциального роста.

* * *

У каждого из нас двое родителей, четверо бабушек-дедушек, восемь прародителей, 16 прапрародителей и т. д. С каждым переходом на поколение назад число предков по прямой линии удваивается. Аналогии с легендой о персидских шахматах очевидны. Допустим, поколения сменяются каждые 25 лет. Тогда 64 поколения укладываются в 64 × 25 = 1600 лет (столько лет назад Древний Рим приблизился к своему краху). Выходит, каждый из ныне живущих должен был иметь в 400 г. н. э. около 18,5 квинтиллиона предков (см. врезку)? Причем без учета родственников по боковым линиям. Но это намного больше всего населения Земли, тогдашнего и нынешнего, намного больше суммарного числа когда-либо живших людей. Где же ошибка? В предпосылке, что все наши прямые предки – разные люди. Разумеется, это не так. К одному и тому же предку восходит множество линий наследования. С каждым мы соединены многими пересекающимися родственными связями. По мере продвижения вглубь времен число пересечений становится огромным.

Это относится ко всему человечеству. Достаточно углубившись в прошлое, можно найти общего предка любых двух людей на Земле. Всякий раз, как избирается новый президент США, кто-нибудь – как правило, в Англии – непременно находит его родственные связи с британской королевой. Считается, что это объединяет носителей английского языка. У двух представителей одного народа или этноса или уроженцев достаточно изолированного региона, имеющих документированную генеалогию, найти общего предка не проблема. Но даже если следы его теряются в дали времен, он обязательно есть. Все мы родичи – абсолютно все, живущие на Земле.

РАСЧЕТ ВОЗНАГРАЖДЕНИЯ, КОТОРОЕ ШАХ ДОЛЖЕН БЫЛ ВЫПЛАТИТЬ ВИЗИРЮ

Давайте подсчитаем, сколько же зерен пшеницы нужно было поместить на шахматную доску из персидской легенды. Не пугайтесь, это не сложно!

Следующий изящный ход позволит нам получить практически точный результат.

Показатель степени говорит, сколько раз мы умножили число 2 само на себя. 2² = 4, 2⁴ = 16, 2¹⁰ = 1024 и т. д. Пусть S – общее количество зерен на доске, от одного зернышка на первой клетке до 263 на 64-й. Тогда, очевидно:

S = 1 + 2 + 2² + 2³ +… + 2⁶² + 2⁶³.

Просто умножив на два обе части уравнения, приведем его к виду:

2S = 2 + 2² + 2³ + 2⁴ +… + 2⁶³ + 2⁶⁴.

Вычтем первое уравнение из второго:

2S – S = S = 2⁶⁴ – 1.

Это и есть ответ.

Чтобы представить размер этого числа, перейдем к обычной десятичной записи. 2¹⁰ – это примерно 1000, или 10³ (с разницей в 2,4 %). Таким образом, 2²⁰ = 2^{(10 × 2)} = (2¹⁰)² = примерно (10³)² = 10⁶, что есть 10, взятые шесть раз, т. е. миллион. Аналогично, 2⁶⁰ = (2¹⁰)⁶ = примерно (10³)⁶ = 10¹⁸. Тогда 2⁶⁴ = 2⁴ × 2⁶⁰ = около 16 × 10¹⁸, или 16 с восемнадцатью нулями – 16 квинтиллионов зерен. Точный расчет дает 18,6 квинтиллиона.

* * *

Еще один яркий пример геометрической прогрессии связан с понятием так называемого периода полураспада. Радиоактивный «материнский» элемент, допустим, плутоний, распадается в дочерний элемент, обычно менее опасный. Это не моментальный процесс, он протекает во времени по определенному закону. Через известный промежуток – период полураспада – распадется половина атомов. Оставшиеся продолжат делиться, по прошествии еще одного такого же временного интервала половина их также распадется и т. д. Например, при периоде полураспада, равном году, половина имеющегося количества атомов распадется через год, половина оставшейся половины, или четверть исходного количества, – через два года, одна восьмая от начального числа – через три года, одна тысячная – через 10 лет и т. д. У каждого элемента свой период полураспада. Этот показатель приходится учитывать при решении проблемы хранения отработавшего топлива АЭС или при расчете радиоактивного заражения местности в ходе ядерной войны. Это пример экспоненциального уменьшения, противоположный представленному в персидской легенде экспоненциальному росту.