Силы притяжения, действующие на тело внутри диска

1. Сила притяжения внутри диска

В результате астрономических наблюдений выяснилось, что звёзды на краю галактик движутся быстрее, чем этого требуют законы Кеплера. Скорости звёзд обобщённо описываются так называемой кривой вращения, то есть, зависимостью скорости объекта от его удалённости от центра галактики. Согласно кривым вращения, звёзды с такими скоростями попросту должны покинуть галактику, но этого не происходит.

Некоторые галактики представляют собой диск переменной толщины, напоминающий скорее спортивный снаряд – диск или две шляпы приложенные друг к другу. В общем случае такой диск галактики можно рассматривать как объект, имеющий разную плотность, в зависимости от удалённости от центра.

Далее мы рассмотрим гипотетическую структуру, некое условное подобие галактики: тонкий, с нулевой толщиной пылеобразный диск радиуса R₀, внутри которого находится точечное тело массой m. Никакой привязки к реальной галактике мы не делаем. Под пылеобразностью диска подразумевается возможность для тел, находящихся внутри него, беспрепятственно двигаться независимо от других его компонент.

Основной целью наших вычислений, исследований является определение возможности по заранее заданной произвольной кривой вращения сформировать такую функцию плотности, которая, собственно, и формирует эту кривую вращения. Если такая процедура возможна, то мнение о том, что движение звёзд на окраине галактик не-кеплеровское, следует, по меньшей мере, признать неточным. Также это будет означать, что такие скорости и вообще любые скорости напрямую связаны с функцией плотности дисковой галактики.

Вычислим силу, действующую на тело m внутри этого диска. Вычисления будем проводить, условно разбив диск на набор обручей, каждый из которых притягивает тело m независимо от других. На следующем рисунке радиус R₀– это радиус всего диска, внутри которого пробное тело m, для которого мы и вычисляем силы, находится на удалении Rx от центра. Считаем, что на пробное тело действуют две условные силы: сила, притягивающая его в центр, суммарная сила от обручей с радиусом, меньшим Rx, и ослабляющая её сила, направленная наружу, от центра диска. Эту ослабляющую силу, очевидно, создают внешние части обручей с радиусом, превышающим Rx. Внешние части обручей – это те, что находятся за координатой Rx.

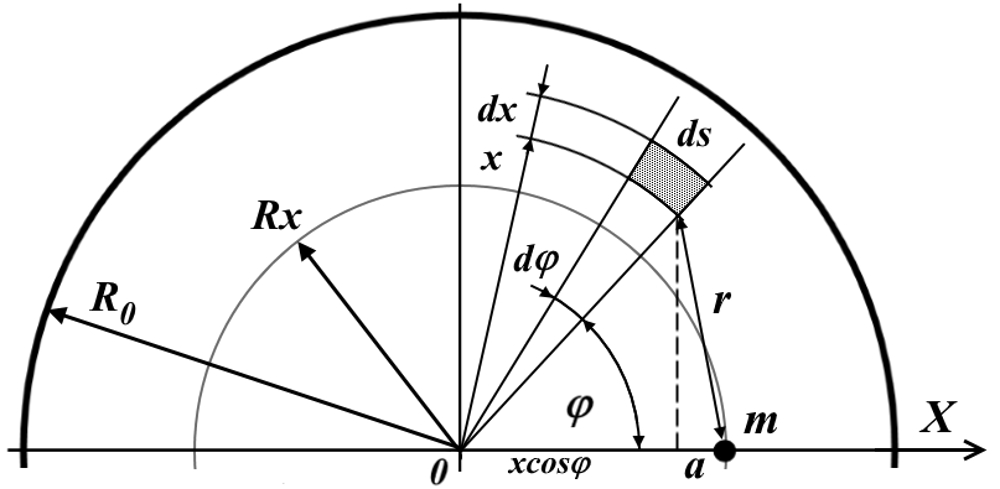
Рис.1.1. Сила притяжения между дифференциалом dM массы диска и пробным телом m внутри диска

Элементарная сила притяжения dF, создаваемая дифференциальным элементом любого обруча равна

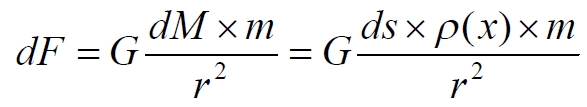
Дифференциал массы обруча определяем через дифференциал площади ds, который равен

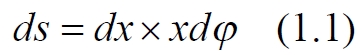
Расстояние r между массой m и дифференциальным элементом

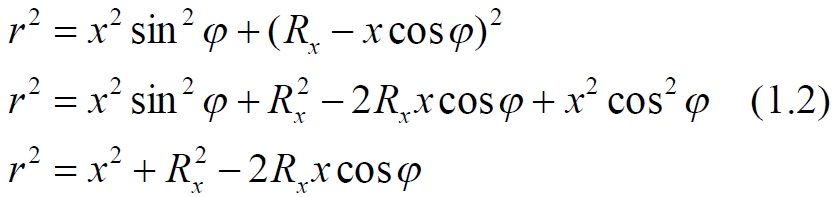
Подставляем (1.1) и (1.2) в уравнение силы

Эта сила имеет две ортогональные составляющие – вдоль оси X и перпендикулярно ей. Перпендикулярные силы, в конечном счете, компенсируют друг друга вследствие симметрии. Нас же интересует только сила, направленная вдоль горизонтальной оси, формирующие общую силу притяжения m в сторону центра диска. Эта составляющая определяется из подобных треугольников

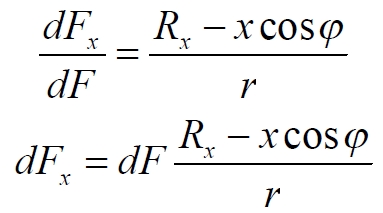
Подставляем величину силы

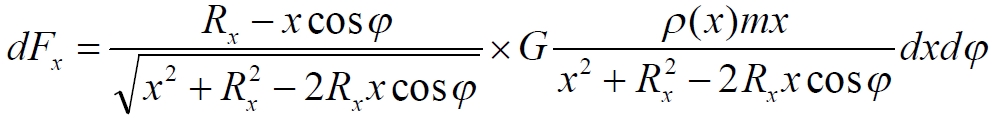
Преобразуем

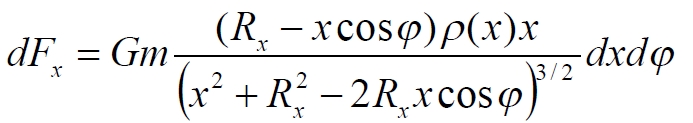
Интегрированием по всему радиусу диска находим полную силу

Это и есть полное значение силы, действующей на m, которое находится в средней части диска. Отметим, что ослабляющая сила тем сильнее, чем ближе m к центру диска. Здесь следует отметить следующее. Рассмотрим сумму в скобках в числителе

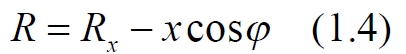
При вычислениях интеграла величина x для некоторого положения тела Rx изменяется в интервале от 0 до R₀ – на полном интервале радиуса диска. Этот интервал x следует формально разделить на два участка. На первом участке всегда x ≤ Rx, на втором – всегда x > Rx. Это приводит к тому, что в первом случае величина (1.4) и соответствующий ей интеграл в (1.3) оказывается положительной величиной всегда, а во втором, при некоторых углах φ, величина (1.4) и соответствующий ей интеграл в (1.3) становятся отрицательными. На знак интеграла знаменатель влияния не оказывает, поскольку сумма квадратов величин всегда больше их удвоенного произведения. Действительно, максимальное значение отрицательного слагаемого, способного сделать эту сумму отрицательной, определяется значением косинуса. Максимум отрицательной величины очевиден – это единичное значение косинуса:

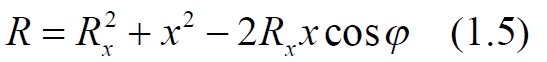
В этом случае получаем уравнение

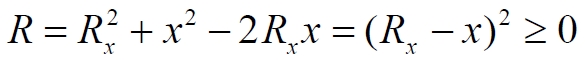
То есть, мы получили величину, которая никогда не принимает отрицательных значений, следовательно, и (1.5) также всегда положительна. Это означает, что при значениях параметра x, для некоторых обручей диска, являющихся для m внешними, сила притяжения при определённых углах φ имеет отрицательные значения, то есть, уменьшает силу притяжения тела в сторону центра диска. Запишем окончательное уравнение для результирующей силы, действующей на пробное тело m