Качественные задачи по физике в средней школе и не только…

Я считаю, что понял смысл уравнения, если в состоянии представить себе общий вид его решения, не решая его непосредственно.

Поль Дирак, один из величайших физиков-теоретиков XX века

© ООО «Издательство АСТ», 2021

© Иллюстрации Подобед В., 2021

Предисловие

Перед вами сборник качественных задач по физике. Слово «качественные» здесь говорит вовсе не о качестве этих задач (хотя они и были тщательно подобраны), а противопоставляет их количественным задачам, то есть задачам, для решения которых требуются расчеты. Качественная задача решается с помощью рассуждений, схем, графиков, иногда экспериментов – но без вычислений (простейшая арифметика не в счет). В то же время не следует путать качественную задачу с «вопросами на закрепление пройденного», которые можно найти почти после каждого параграфа в учебнике: ответы на такие вопросы обычно «спрятаны» в готовом виде где-то в тексте самого параграфа, а вот готовых ответов на качественную задачу в учебнике нет.

К сожалению, преподавание физики в школе порой создает ложное представление о том, как решаются физические задачи: «Нужно найти подходящую формулу, подставить в нее числа и выполнить расчеты». В такой картине мира, конечно, для качественных рассуждений не остается места, поскольку физик здесь выглядит чем-то средним между справочником и приложением к калькулятору. Однако на самом деле решению почти любой содержательной количественной, расчетной физической задачи предшествует решение качественной задачи: физик должен разобраться в явлении, понять, какими физическими законами оно управляется, и составить модель этого явления. И лишь после этого начинаются вычисления – но иногда в них уже нет необходимости (именно об этом говорил Поль Дирак, слова которого вынесены в эпиграф). Другими словами, умение справляться с качественными задачами – очень важный навык настоящего физика, а само противопоставление качественных и количественных задач довольно искусственно.

Чтобы решить качественную задачу, нужно, конечно, хорошо знать и понимать законы физики. Но еще нужно уметь выделять главное и отодвигать в сторону второстепенное, видеть взаимосвязи, рассуждать логически. Вот этому в меру возможности и научит вас сборник задач, который вы держите в руках.

Расположение задач в сборнике в целом повторяет структуру курса физики в средней школе, однако такое деление все же условно и сделано для ориентира: некоторые задачи допускают несколько разных подходов, для решения других нужно скомбинировать физические законы из разных разделов.

В некоторых задачах есть подвох или неожиданный поворот, чтобы напомнить, что физик всегда имеет дело с реальным миром и должен быть готов к тому, что этот мир не вполне укладывается в готовые схемы. По той же причине условия задач далеки от рафинированного «тело массы m равномерно движется по абсолютно гладкой поверхности…». Даже когда герои задачи выдуманы (здесь вас ждут и три поросенка, и Золушка, и Гэндальф с Бильбо Бэггинсом, и вездесущий Мюнхгаузен, и друзья-физики Винкель и Нуллибер – кстати, догадаетесь ли вы, откуда взялись их имена?), сама физическая ситуация вполне реалистична. Физик должен уметь прокладывать путь от практической ситуации к теоретической модели, которая позволит ему применить свои знания физических законов.

Все задачи в этом сборнике (их ровно 200) сопровождаются подробным разбором. Этот разбор если и не приводит прямиком к ответу, то по крайней мере указывает путь. Однако не торопитесь обращаться к разбору – попытайтесь решить задачу самостоятельно. Не отчаивайтесь, если не добьетесь успеха с первой попытки: пользу приносит не обладание ответом, а его поиск. Попробуйте сами задать себе «наводящие» вопросы:

– С какими физическими явлениями имеют дело герои задачи? Какие физически законы управляют этими явлениями?

– Что мне известно? Какие выводы я могу сделать из того, что мне известно?

– Что мне нужно выяснить? Как я мог бы это выяснить? Какая информация мне помогла бы?

Ответы помогут вам совершить следующий шаг.

Усилия, которые вы приложите, даже если они и не приведут вас к ответу, сделают вас немножко более тренированным. Более того, если вы теперь обратитесь к готовому решению (это совершенно не зазорно после того, как вы потратили на обдумывание задачи достаточно сил и времени), вы воспримете его совершенно иначе: «Ах вот в чем тут было дело!» или «Вот чего мне не хватало!». Это и значит, что вы научились чему-то новому для себя.

Чтобы усилить этот эффект, большинство задач в сборнике сделаны многослойными, наподобие луковицы или матрешки: читая разбор задачи, вы «в нагрузку» к ответу получаете новые вопросы, которые потребуют дальнейшего обдумывания, а возможно, расчетов или даже углубления теоретических познаний.

Хочется надеяться, что работа с этим сборником поможет вам лучше разглядеть красоту, многогранность и практичность физики и понять, почему для многих она становится делом жизни. Может быть, и вы присоединитесь к их числу!

Условия задач

I. Знакомство с физикой

1. Физические измерения

1. Приумножить и измерить

Представьте себе, что вам понадобилось измерить толщину троса, но никакого измерительного прибора, кроме линейки, у вас под рукой не оказалось, а точность «плюс-минус миллиметр» вас не устраивает. Как провести точное измерение толщины троса обычной линейкой?

2. Винкель на диете

Винкель по настоянию врача сел на диету. Среди условий диеты есть ограничение на количество черешни (которую Винкель, как назло, очень любит): врач настоятельно рекомендовал ему съедать не больше 200 мл черешни в день. Винкель, конечно, мог бы просто насыпать черешню в обычный стакан, объем которого как раз 200 мл, однако в стакане между ягодами есть пустоты. Винкель не готов нарушать предписания врача, но и пустоты его очень огорчают: ведь это означает, что объем черешни в стакане меньше 200 мл. Помогите Винкелю отмерить нужное количество черешни.

2. Строение вещества

3. Дружные стекла

Почему трудно отделить друг от друга два больших стекла, сложенных вместе?

4. Горячий и сладкий

Почему сахар быстрее растворяется в горячем чае, чем в холодном?

5. Можно ли сделать из мухи слона?

В фильмах ужасов и фантастических фильмах нередко появляются насекомоподобные существа очень крупных размеров (размером с человека или даже больше). Может ли теоретически существовать муха размером со слона (скажем, как результат генетической мутации)?

II. Движение тел

3. Поступательное движение. Скорость. Путь

6. Три гонца и один график

Взбалмошный король Тридевятого королевства послал к царю Тридесятого царства конного гонца с объявлением войны. Первый гонец еще не успел вернуться, как король передумал и отправил вслед предложение о перемирии с еще одним гонцом, который поехал верхом на осле, потому что скакун в королевстве был всего один. Вкусный ужин окончательно примирил короля с действительностью, и, не дожидаясь возврата первых двух посланников, король составил предложение своей руки и сердца, предназначенное царевне Тридесятого царства. За недостатком транспортных средств это предложение понес пеший посланник.

Скорости всех гонцов постоянны, конный гонец движется быстрее всех, а пеший – медленнее всех, в Тридесятом царстве гонцы не задерживаются, а сразу отправляются домой. Дорога между Тридевятым королевством и Тридесятым царством всего одна, а при встрече гонцов более быстрый забирает послание у более медленного и поворачивает назад, чтобы ускорить доставку дипломатической почты.

Кто из гонцов доставит царевне предложение руки и сердца?

7. Сначала подумать, потом побежать

В точке A на пляже (рис. 1) располагается вышка спасателя, в точке B в море начинает тонуть человек.

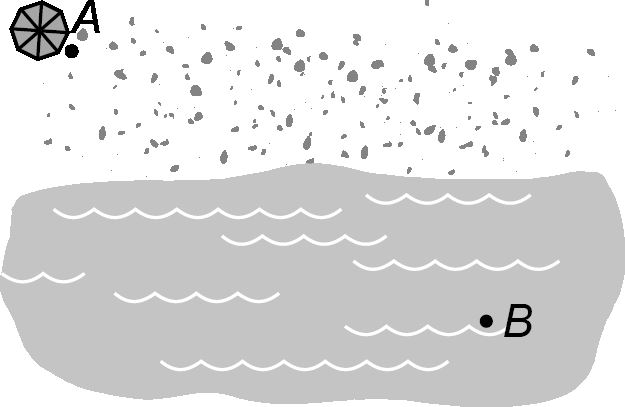
Рис. 1

Спасатель, хотя и является профессиональным пловцом, плывет медленнее, чем бежит. Какую траекторию движения ему следует выбрать, чтобы оказаться рядом с тонущим как можно быстрее?

8. Мюнхгаузен на скачках

– …В самом конце первого круга моя лошадь подвернула ногу, но я не растерялся, взвалил ее на плечи и второй круг пробежал, неся лошадь на себе. Поскольку мы финишировали с нею вместе, опередив всех, судьи были вынуждены засчитать нам победу – ведь неважно, кто был на ком!

– Вы хотите сказать, барон, что бежали с лошадью на плечах быстрее фаворита скачек?

– Ну что вы, конечно нет. Впрочем, фаворит в тот день был не в форме и бежал со скоростью 30 верст в час, а прочие и того хуже.

– Но для человека с грузом и это недостижимая скорость!

– Разумеется. Даже я с такой ношей вряд ли развиваю больше 15 верст в час. Просто моя лошадь очень хорошо прошла первый круг!

Разоблачите барона Мюнхгаузена.

9. Рассеянный локомотив

Локомотив с единственным вагоном въехал на очень длинный мост. В момент въезда на мост вагон отцепился и стал замедляться с постоянным по величине ускорением, а локомотив продолжил движение, не меняя скорости. Вагон остановился посередине моста. Где в этот момент оказался локомотив?

4. Вращательное движение

10. Загадка железнодорожных колес

Металлические колеса железнодорожного вагона, трамвая, поезда метро напрессовываются на металлическую же ось, так что образуется жесткая конструкция – так называемая колесная пара. Однако на повороте рельсового полотна внешнее колесо должно пройти больший путь, чем внутреннее, то есть сделать больше оборотов вокруг своей оси. Но это физически невозможно, потому что колеса на оси зафиксированы. Проскальзывание колеса по рельсу – явление неприятное и небезопасное. Как решается эта проблема?

11. Транспортировочная суета

В древности тяжелые грузы часто перемещали на помостах, под которые подкладывали бревна. Люди или животные тянули помост вперед, он перекатывался на бревнах, бревно, которое выкатывалось из-под помоста сзади, переносили (или перекатывали) и подкладывали спереди (рис. 2).

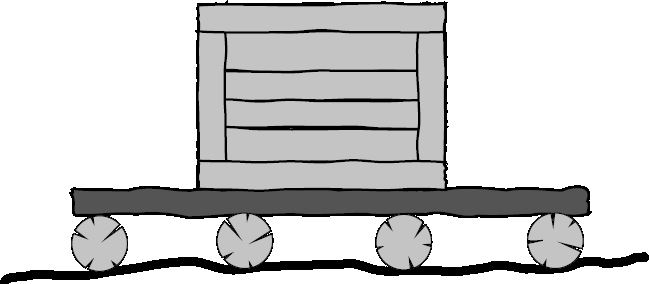
Рис. 2

Винкель и Нуллибер решили устроить реконструкцию древнего строительства и перемещают трехметровый помост на четырех бревнах (это минимальное количество, обеспечивающее устойчивость: почти все время помост катится на трех бревнах, пока четвертое переносят). Помост преодолел сто метров. Сколько раз друзьям придется перенести вперед бревно, выкатившееся сзади? Какое суммарное расстояние они пройдут за это время с бревном?

12. Кроличьи бега

Шесть глупых и жадных кроликов сидят в вершинах правильного шестиугольника в темной комнате и грызут по морковке. Когда включают свет, каждый кролик замечает, что у соседа справа есть морковка, и преисполняется желания ее отобрать, то есть каждый кролик начинает бежать к своему соседу справа. Чем все это закончится?

13. Шустрая грязь

На колеса велосипеда устанавливают щитки, которые защищают велосипедиста от грязи, слетающей с колес. Грязь слетает с колеса с той скоростью, до которой ее разогнало колесо. Понятно, почему на велосипедиста попадает грязь с переднего колеса. Но зачем нужен щиток на заднем – ведь для того, чтобы попасть с заднего колеса на спину велосипедиста, грязь должна обогнать велосипед, то есть двигаться со скоростью больше скорости велосипеда? Как это возможно?

14. Сложное движение велосипеда

Куда движутся педали велосипеда относительно рамы, когда велосипедист работает ногами и велосипед едет вперед? А относительно земли? Относительно верхней точки колеса?

15. Вперед или назад?

Во время поездки на поезде Винкель сказал Нуллиберу, что прямо сейчас у их поезда есть части, которые движутся в обратном направлении – против хода поезда. Нуллибер предположил, что это дым из трубы, но Винкель напомнил ему, что магистральные железные дороги давно электрифицированы. Тогда Нуллибер сказал, что Винкель говорит ерунду. Кто из друзей прав?

III. Взаимодействие тел

5. Инерция. Силы. Законы Ньютона

16. Мокрый зонт

Зачем перед тем, как войти в помещение, мокрый зонт встряхивают. Какие физические закономерности при этом используются?

17. Загадочный топор

Сейчас почти любое туристическое снаряжение можно купить в магазине, но несколько десятилетий назад туристы многое изготавливали своими руками. Часто можно было увидеть походный топор, в котором вырезана часть щеки (два варианта показаны на рис. 3 – удачный и не очень удачный).

Рис. 3

Зачем это делалось? Какие недостатки есть у такого топора?

18. Потерявшаяся сила

На письменном столе лежит учебник физики. Как на любое тело, обладающее массой, со стороны земного шара на этот учебник действует сила гравитационного притяжения. Назовите парную ей силу с точки зрения третьего закона Ньютона («силу противодействия»).

19. Трактор против скалы

В каком случае канат порвется скорее: если его концы привязать к двум одинаковым тракторам, тянущим в противоположные стороны, – или если один конец привязать к такому же трактору, а другой прикрепить к скале?

20. Между молотом и диваном

Почему грецкий орех легко расколоть молотком на столе, но невозможно на мягком диване? Почему на столе это легче сделать, если молотком ударить, а не надавить?

21. Как по маслу!

Когда мы режем ножом продукты, в большинстве случаев мы не просто давим на нож сверху вниз, а проводим им вперед и назад. Это привычное действие, о смысле которого мы никогда не задумываемся. Однако так резать действительно легче (вы можете проверить это экспериментально). Почему?

22. Как сделать склон пологим

Автомобилю не хватает мощности, чтобы въехать на невысокий, но протяженный и довольно крутой склон (рис. 4).

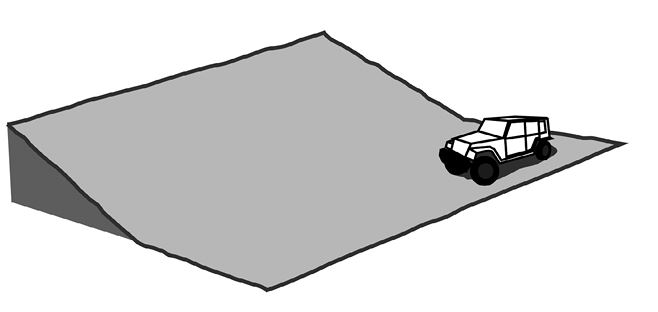
Рис. 4

Как можно справиться с этой проблемой?

23. Как сделать склон пологим – 2

Опытные водители, припарковавшись на улице, идущей в гору или под гору, полностью выворачивают руль в одну или в другую сторону. Зачем?

24. Занимательные подтягивания

Как расположить руки на перекладине турника (ближе друг к другу? дальше? насколько ближе или дальше?), чтобы подтягиваться было легче?

25. Очень ровная веревка

Можно ли натянуть веревку между двумя столбиками так, чтобы она совсем не провисала?

26. Рвется там, где… толсто!

Винкель выстирал свой свитер, расправил его на старой вешалке с веревочкой вместо крючка, и повесил вешалку на гвоздик. На полу под свитером быстро собралась лужа, и Винкель решил перевесить свитер на бельевую веревку на улице. К его удивлению, бельевая веревка оборвалась, хотя была гораздо толще и прочнее веревочки на вешалке. Почему тонкая веревочка выдержала вес свитера, а толстая бельевая веревка – нет?

6. Вес, масса, сила тяжести

27. Цельтесь выше!

Если вам доводилось стрелять в тире из пневматической винтовки, вам наверняка сообщили этот нехитрый секрет: целиться нужно немного выше той точки, в которую вы хотите попасть. Почему?

28. Хитрая обезьяна

Индеец, сидя в засаде в кустах, стреляет из лука в обезьяну, висящую на ветке дерева. Обезьяна очень внимательна и обладает быстрой реакцией, так что, услышав шорох вылетевшей стрелы, сразу разжимает руки и падает. Индеец хорошо знаком с повадками обезьяны и знает, что сразу после выстрела она отпустит ветку. Как ему нужно целиться, чтобы попасть: прямо в обезьяну, выше или ниже?

29. Перетягивание космонавта

Есть довольно большая группа людей, убежденных в том, что люди никогда не высаживались на Луне, а имеющиеся фото- и видеоматериалы – это «съемка в голливудских павильонах». В обоснование своей точки зрения они приводят различные доводы, часть из которых имеет отношение к физике. Вот один из них: Земля примерно в 80 раз массивнее Луны. По закону всемирного тяготения ее притяжение тоже должно быть гораздо сильнее лунного. Значит, космонавты не смогли высадиться на Луне и ходить по ее поверхности: они бы «воспарили» под действием земного притяжения.

В чем ошибка?

30. Ошибка Жюля Верна

В романах «С Земли на Луну прямым путем», «Вокруг Луны» и «Вверх дном» французский писатель-фантаст XIX века Жюль Верн описывает путешествие на Луну, которое персонажи этих произведений совершили в корабле-снаряде, запущенном из огромной пушки на Земле. Покинув пушку, снаряд дальше должен был лететь по инерции до самой Луны. Вот фрагмент описания этого полета:

«Путь снаряда лежал между Землей и Луной. По мере того как снаряд удалялся от Земли, земное притяжение изменялось обратно пропорционально квадрату расстояния. Лунное же притяжение изменялось прямо пропорционально. В какой-то точке пути оба притяжения – лунное и земное – должны были уравновеситься, и тогда снаряд должен был потерять всякий вес. Если бы массы Луны и Земли были одинаковы, эта точка находилась бы как раз на середине расстояния между обеими планетами. Но так как массы их различны, то легко вычислить, что эта точка находилась на части всего пути, или в численном выражении в 78 114 лье от Земли.

<…>

До сих пор путешественники хотя и знали, что земное тяготение постепенно убывает, однако не могли еще заметить полного его исчезновения. Но как раз в этот день утром, около одиннадцати часов, Николь уронил стакан, и, к общему изумлению, стакан не упал, а повис в воздухе.

– Вот так штука! – воскликнул Ардан. – Вот тебе и законы физики!

Действительно: различные предметы, оружие, бутылки, брошенные и предоставленные самим себе, словно чудом держались в воздухе».

Что не так в этом тексте с точки зрения физики?

31. Нуллибер изучает свой вес

Нуллибер встал на напольные весы – и они показали 99 кг. Как изменится этот результат, если Нуллибер будет взвешиваться в равномерно поднимающемся лифте? В лифте, который поднимается и набирает скорость? В лифте, который поднимается и снижает скорость, чтобы остановиться? В лифте, который движется вниз и набирает скорость? В падающем лифте?

32. Переступить предел

За транспортировку багажа весом больше 20 кг в аэропорту приходится доплачивать. Винкель подозревает, что вес его чемодана может превысить этот предел, однако проверить это не так просто: к весам для взвешивания багажа выстроилась длинная очередь. Заметив, как Винкель нервничает, Нуллибер достает из своего рюкзака весы-безмен и кусок капроновой веревки. Винкель радуется, но радость его быстротечна:

– У твоего безмена шкала заканчивается на 12 килограммах, – уныло говорит он.

– А нам больше и не надо! – хитро улыбаясь, отвечает Нуллибер. Что он придумал?