1. Основные понятия. Системы координат. Прямые линии и их взаимное расположение
Координата точки – это величина, определяющая положение данной точки на плоскости, на прямой или кривой линии или в пространстве. Значение координаты зависит от выбора начальной точки, от выбора положительного направления и от выбора единицы масштаба.
Прямоугольная система координат состоит из двух взаимно перпендикулярных прямых – осей, точка их пересечения – начало координат О, ось ОХ – ось абсцисс, ось ОY – ось ординат. На осях выбираются масштаб и положительное направление.

Рис. 1
Системы координат
Положение точки М определяется двумя координатами: абсциссой х и ординатой у. Записывается так: М(х, у). Оси координат образуют четыре координатных угла I, II, III, IV. Если точка находится в I координатном угле (квадранте), то и абсцисса, и ордината ее положительные, если – во II квадранте, то абсцисса отрицательна, а ордината положительна, если в – III квадранте, и абсцисса, и ордината отрицательны, если – в IV квадранте, положительна абсцисса, а ордината отрицательна. У точки, лежащей на оси ординат, абсцисса равна нулю, и наоборот, если точка лежит на оси абсцисс, то ее ордината равна нулю.
Косоугольной системой координат аналогична прямоугольной, только оси координат пересекаются под углом не равным прямому. Прямоугольная и косоугольная системы относятся к декартовой системе координат.
Полярная система координат состоит из полюса О и полярной оси ОХ, проведенной из полюса. Положение точки определяется полярным радиусом ρ (отрезок ОМ) и полярным углом φ. Для полярного угла берется его главное значение (от –π до π). Числа ρ, φ называются полярными координатами точки М.
Связь между координатами точки в прямоугольной и полярной системах координат: x = r cosφ, y = r sinφ или:


Пусть имеются две точки М1(х1, у1) и М2(х2, у2). Расстояние между точками:
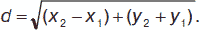
Общее уравнение прямой линии (система координат прямоугольная): Ах + Ву + С = 0 (А и В одновременно не равны нулю).
Если В не равно нулю, то уравнение прямой: у = ах + b (здесь а = – А / В, b = – С / В). Здесь а есть тангенс угла наклона прямой к положительному направлению оси абсцисс, b равно длине отрезка от начала координат до точки пересечения рассматриваемой прямой с осью ординат. Уравнение прямой, параллельной оси абсцисс: у = b, уравнение оси абсцисс: у = 0; уравнение прямой, параллельной оси ординат: х = с, уравнение оси ординат: х = 0.
2. Условие нахождения трех точек на одной прямой. Уравнение прямой. Взаимное расположение точек и прямой. Пучок прямых. Расстояние от точки до прямой
1. Пусть даны три точки А1 (х1, у1), А2 (х2, у2), А3 (х3, у3), тогда условие нахождения их на одной прямой:
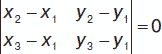
либо (х2 – х1) (у3 – у1) – (х3 – x1) (у2 – у1) = 0.
2. Пусть даны две точки А1 (х1, у1), А2 (х2, у2), тогда уравнение прямой, проходящей через эти две точки:

(х2 – х1)(у – у1) – (х – х1)(у2 – у1) = 0 или (х – х1) / (х2 – х1) = (у – у1) / (у2 – у1).
3. Пусть имеются точка М (х1, у1) и некоторая прямая L, представленная уравнением у = ах + с. Уравнение прямой, проходящей параллельно данной прямой L через данную точку М:
у – у1 = а(х – х1).
Если прямая L задана уравнением Ах + Ву + С = 0, то параллельная ей прямая, проходящая через точку М, описывается уравнением А(х – х1) + В(у – у1) = 0.
Уравнение прямой, проходящей перпендикулярно данной прямой L через данную точку М:
у – у1 = –(х – х1) / а
или
а(у – у1) = х1 – х.
Если прямая L задана уравнением Ах + Ву + С = 0, то параллельная ей прямая, проходящая через точку М(х1, у1), описывается уравнением А (у – у1) – В(х – х1) = 0.
4. Пусть даны две точки А1 (х1, у1), А2 (х2, у2) и прямая, заданная уравнением Ах + Ву + С = 0. Взаимное расположение точек относительно этой прямой:
1) точки А1, А2 лежат по одну сторону от данной прямой, если выражения (Ах1 + Ву1 + С) и (Ах2 + Ву2 + С) имеют одинаковые знаки;
2) точки А1, А2 лежат по разные стороны от данной прямой, если выражения (Ах1 + Ву1 + С) и (Ах2 + Ву2 + С) имеют разные знаки;
3) одна или обе точки А1, А2 лежат на данной прямой, если одно или оба выражения соответственно (Ах1 + + Ву1 + С) и (Ах2 + Ву2 + С) принимают нулевое значение.
5. Центральный пучок – это множество прямых, проходящих через одну точку М (х1, у1), называемую центром пучка. Каждая из прямых пучка описывается уравнением пучка у – у1 = к (х – х1) (параметр пучка к для каждой прямой свой).
Все прямые пучка можно представить уравнением: l(y – y1) = m(x – x1), где l, m – не равные одновременно нулю произвольные числа.
Если две прямые пучка L1 и L2 соответственно имеют вид (А1х + В1у + С1) = 0 и (А2х + В2у + С2) = 0, то уравнение пучка: m1(А1х + В1у + С1) + m2(А2х + В2у + С2) = 0. Если прямые L1 и L2 пересекающиеся, то пучок центральный, если прямые параллельны, то и пучок параллельный.
6. Пусть даны точка М (х1, у1) и прямая, заданная уравнением Ах + Ву + С = 0. Расстояние d от этой точки М до прямой:
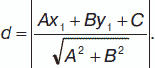
3. Полярные параметры прямой. Нормальное уравнение прямой. Преобразование координат
Полярными параметрами прямой L будут полярное расстояние р (длина перпендикуляра, проведенного к данной прямой из начала координат) и полярный угол α (угол между осью абсцисс ОХ и перпендикуляром, опущенным из начала координат на данную прямую L). Для прямой, представленной уравнением Ах + Ву + С = 0: полярное расстояние

полярный угол α
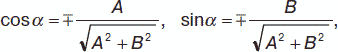
причем при C > 0 берется верхний знак, при C < 0 – нижний знак, при С = 0 знаки берутся произвольно, но либо оба плюса, либо оба минуса.
Нормальное уравнение прямой (уравнение в полярных параметрах) (cм. рис. 2): x cosα + y sinα – p = 0. Пусть прямая представлена уравнением вида Ах + Ву + С = 0. Чтобы данное уравнение привести к нормальному виду необходимо последнее разделить на выражение  (знак берется в зависимости от знака С).
(знак берется в зависимости от знака С).

Рис. 2
После деления получается нормальное уравнение данной прямой:

Пусть имеется прямая L, которая пересекает оси координат. Тогда данная прямая может быть представлена уравнением в отрезках х / а + у / b = 1. Справедливо: если прямая представлена уравнением х / а + у / b = 1, то она отсекает на осях отрезки а, b.
Преобразование координат возможно путем переноса начала координат, или поворотом осей координат, или совместно переносом начала и поворотом осей.
При переносе начала координат справедливо следующее правило: старая координата точки равна новой, сложенной с координатой нового начала в старой системе. Например, если старые координаты точки М были х, у, а координаты нового начала в старой системе О*(х0, у0), то координаты точки М в новой системе координат с началом в точке О* будут равны х – х0, у – у0 т. е. справедливо следующее х = х* + х0, у = у* + у0 или х* = х – х0, у* = у – у0 (* новые координаты точки).
При повороте осей на некоторый угол φ справедливы следующие формулы (где х, у – старые координаты точки; х*, у* – новые координаты этой же точки):
x = x* cosα – y* sinα;
y = x* sinα + y* cosα
или
x* = x cosα + y sinα;
y* = – x sinα + y cosα.

