Часть 1. Ликбез
1.0. Загадка индукционного датчика
В давние-стародавние времена, когда интернета ещё и в помине не было, возник у нас с одним креативным малым дерзкий проект. Вознамерились мы обессмертить свои имена созданием безрезонансного датчика для электрогитары. По нашему разумению, резонанс датчика является нежелательным, ибо затрудняет эквализацию сигнала.
Откуда этот резонанс берётся? Катушка датчика представляет собой индуктивность (L), это совершенно очевидно, менее очевидно, но факт, что между витками возникает ёмкость (C). A LC – это знакомый нам со школы колебательный контур, имеющий собственную частоту. Вот этот «недостаток» мы и решили устранить.
Идея была проста, как всё гениальное: секционированием катушки повысить её собственную частоту выше пределов слышимого, создав во всём слышимом диапазоне почти линейную АЧХ. Секционированная катушка не была нашим изобретением, в радиоприёмной аппаратуре их применяли много лет. Свою заслугу мы видели в идее применения такого решения в гитарном датчике.
Сказано-сделано, и… результат не понравился ни одному гитаристу. Да что там, нам самим звучание не понравилось. Мы пытались исправить дело эквалайзерами, но это ничего не дало.
Другой смелый эксперимент я проводил в одиночку. Это была приставка к электрогитаре для улучшения звучания путём пропускания звука через акустическую древесину. И снова ничего! Электромагнит исправно передавал колебания еловой деке с наклеенными стальными пластинами, датчик эти колебания исправно снимал, а звук нисколько не становился похожим на звук акустической гитары.
В те же времена в некоторых кругах возник спор, который и ныне продолжается уже на страницах интернета: влияет ли несущая конструкция электрогитары на звучание? Сторонники влияния никак не обосновывают свои утверждения теоретически, они исходят из субъективных ощущений, а вот их оппоненты приводят массу аргументов.
Например: некоторые фирмы делают грифы электрогитар из углепластика, другие делают корпуса из ДВП. Другой аргумент: амплитуда колебаний деки электрогитары во много раз меньше амплитуды колебаний струн, их даже не видно. А ещё в интернете есть ролик, где тестируют стратокастер с деревянным и пластмассовым корпусами, звучание невозможно отличить… А в дискуссиях они задают оппонентам риторический вопрос: «А ты сможешь определить по звучанию, из какого дерева сделана дека электрогитары?» И тем нечем крыть!
Однозначно, не влияет!!!
Вот только… На акустической гитаре колебания деки так же микроскопичны, и глазом не видны. А в интернете есть ролик, где тестируют два «дредноута», один деревянный, другой – пластмассовый, и звучание тоже один в один. И в слепом прослушивании материал акустической деки вы тоже не сможете определить.
И какой вывод? Может быть, и в акустических гитарах несущая конструкция не влияет на звучание? Нет, вывод, что все эти аргументы несостоятельны.
И конечно же, коронный аргумент невлияльщиков: индукционный датчик не преобразует колебания немагнитной деки в ЭДС! Похоже, в школе физику не прогуливали. Правда, и подключенную электрогитару в руках не держали. И на вопрос, почему разные электрогитары звучат так по-разному, у них готов ответ: всё дело в датчиках. Но вопрос, каковы должны быть параметры хорошо звучащего датчика, повергает их в ступор.
Да, знания за среднюю школу здесь недостаточны, чтобы найти ответы на все эти вопросы, надо изучить физику колебательных явлений посерьёзней, чем она даётся в школьной программе.
1.1 Атака и сустейн
Звучание струны состоит из двух фаз – атака и затухание. Обе фазы протекают по графику логарифмической функции, иначе говоря, по экспоненте. Длительность затухания называют сустейном, и характеризуют временем, в течение которого амплитуда колебаний струны понижается на 30 децибел.
Наиболее важна для восприятия характера звучания фаза атаки. В давние времена проводился эксперимент: из магнитофонной записи звучания разных инструментов удалили фазу атаки, так при прослушивании таких фонограмм профессиональные музыканты саксофон от рояля не могли отличить. Вывод: характер звучания инструмента формируется на стадии атаки.
***
Сустейн зависит от многих факторов, как в струне, так и в несущей конструкции.
Чем выше добротность струны, сильнее натяжение, тем сустейн будет длительней, а атака ярче.
Чем выше упругое сопротивление несущей конструкции, и больше длина рабочей части струны, тем сустейн длительней, а атака мягче.
Поскольку затухание протекает по экспоненте, его можно характеризовать через основание логарифмической функции, взяв шаг во времени, равный периоду колебания. Эта величина получила название логарифмический декремент затухания.
Логарифмическим декрементом затухания называется натуральный логарифм отношения двух последовательных амплитуд, взятых через период.
Обозначается греческой буквой лямбда,
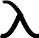
но в тексте буду использовать аббревиатуру ЛДЗ.
1.2. Резонансы и обертоны
Со школьных лет, а кто и раньше, мы помним притчу про солдат, что по мосту шли строем в ногу, и рухнул мост… Ну как же так!
В дискуссиях по музыкальным инструментам в интернете мне не единожды советовали учить физику, высказывая уверенность, что в школе я её не учил. На таких «советчиков» быстро нашёлся приём: определение резонанса помните? Хорошо, а почему такое происходит? Что с неким физическим телом на некоторой частоте не так, как на любой другой? Почему при воздействии сравнительно небольших усилий с некой частотой рухнул мост, способный выдерживать в разы большие статичные нагрузки?
Ни один из самонадеянных оппонентов ответить не смог. Да, друзья, пятёрка по физике в школьном аттестате не делает вас экспертами в технических областях знаний, в том числе в музыкальной акустике. Резонанс в школе не изучают, а именно проходят.
Чтобы найти ответ на этот каверзный вопрос, снова вспомним про колебательный контур, который в школе так же проходили. КК имеет собственную частоту, и может использоваться в электронном генераторе колебаний в качестве частотозадающего узла. А ещё, если через него пропустить несколько сигналов различных частот, мы можем обнаружить, что лучше всего, с наименьшими потерями по амплитуде, будет проходить сигнал с той самой частотой, которую КК задаёт в генераторе.
И что это значит? А это значит, что на резонансной частоте КК имеет минимальное электрическое сопротивление. И если правильно сформулировать причинно-следственную связь, получим определение: резонансная частота колебательного конура это такая частота, на которой его электрическое сопротивление минимально.
От электроники перейдём к механике. Многие физические тела имеют заметный резонанс на определённых частотах. И теперь нам несложно догадаться, откуда он берётся. Да, механическое (упругое) сопротивление физического тела неодинаково на разных частотах, и его резонансная частота – это частота, на которой упругое сопротивление минимально.
Вспомним школьную шутку про электрический ток: он похож на лентяя, поскольку стремится идти по пути наименьшего сопротивления. Вот и свободное колебание тоже норовит сформироваться на частоте, встречающей наименьшее сопротивление, хоть электрическое, хоть механическое.
Сопротивление на резонансной частоте обязательно ниже, чем при статичной нагрузке, в некоторых случаях во много раз. А упругое сопротивление чётко связано с пределом прочности. Разумеется, музыкальные инструменты делаются с достаточным запасом прочности, чтобы не рассыпались от собственного звучания, это для лучшего понимания явления. Например, почему же развалился мост из легенды.
***
Если руководствоваться параллелью с колебательным контуром, резонанс у физического тела может быть только один. Выходит, у струны может быть только один тон, у несущей только один резонанс.
К счастью, это не так. У колебательного контура электронный резонанс действительно один, а вот у физических тел график частота-упругое сопротивление зачастую имеет весьма замысловатую форму, в которой помимо глобального минимума присутствуют ещё и локальные. Такие точки на этом графике, из которых что вверх по частоте, что вниз, сопротивление увеличивается, и соответствуют частотам резонансов. При этом, чем выше абсолютное значение сопротивления в точке некоторого локального минимума, тем слабее резонанс на данной частоте.
Здесь снова уместна параллель из электротехники: так же распределяется мощность между несколькими параллельными резисторами с разным сопротивлением.
Вот так в струнах возникают линейки обертонов, а несущая часть обычно имеет несколько резонансов. Взаимодействие гармоник струн и резонансов несущей части почти всецело определяет звучание инструмента.
1.3. Взаимодействие резонансов
Проведём лабораторную работу. Для неё нам потребуются:
Гитарный тюнер и тюнер для настройки ударных инструментов, скачанные и установленные в компьютере, струна, лучше всего нейлоновая (даже не карбоновая), колок, кое-какие дощечки и брусочки.
Сделаем вот такой «стенд»:
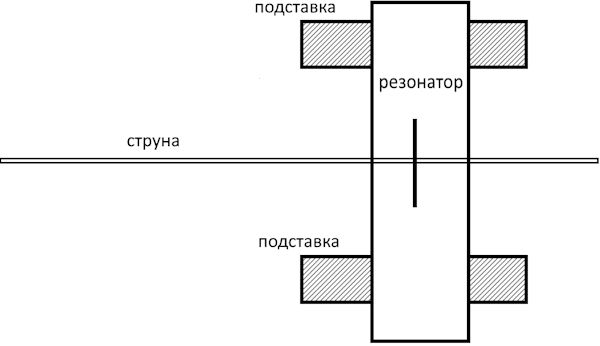
Для начала нам надо добиться унисона между струной и резонатором. Когда вы его добьётесь, поймёте это по ужасному звучанию. Запомните его, это «волчок», о нём ещё поговорим. А теперь понемногу будем сдвигать брусочки, понижая или повышая тон резонатора, при этом каждый раз замеряя тюнером тон струны.
И что обнаружим? Тон струны изменяется вслед за изменением тона резонатора! Но чем дальше мы смещаем тон резонатора, тем отклонение тона струны от первоначального становится меньше.
Объясняется это просто: струна и резонатор образуют единую колебательную систему, и их графики частота-упругое сопротивление складываются. При этом минимумы находятся не на одной и той же частоте, суммарный минимум оказывается где-то между исходными. Несколько сложнее понять, почему этот минимум всегда находится ближе к частоте струны, причём разница может быть во много раз. Для этого надо изучить такой параметр, как добротность (обозначается «Q»).
Добротность пропорциональна числу колебаний, совершаемых системой за время, в течение которого амплитуда уменьшается в е раз. Таким образом, добротность и ЛДЗ являются обратно пропорциональными величинами.
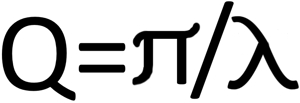
Понятно, что чем выше добротность, например, струны, тем длительней сустейн. А ещё чем выше добротность, тем уже и острее будет диаграмма частота-упругое сопротивление. В результате, при одинаковом отклонении от частоты резонанса, упругое сопротивление у более добротного тела возрастёт больше. Поэтому относительно низкодобротная дека нормально воспринимает колебания в широком диапазоне частот, а высокодобротные струны допускают очень небольшие отклонения.
Девиациям подвергается не только основной тон, но и обертоны. В спектре одной ноты или аккорда одни обертоны завышаются, другие занижаются.
1.4. Динамическая эквализация
Мы знаем, что чем меньше упругое сопротивление несущей конструкции, тем сильнее атака, и короче сустейн в струне. Знаем так же, что резонанс представляет собой перепад упругого сопротивления на частотной шкале.
Логично предположить, что различные гармоники отдельно взятой ноты, встречая разное значение упругого сопротивления, так же будут отличаться по скорости нарастания и последующего убывания амплитуды. И даже переход из фазы нарастания в фазу убывания будет происходить не одновременно.
Да, чем меньше упругое сопротивление несущей на некоторой частоте, тем гармоника с данной частотой будет быстрее нарастать и убывать по амплитуде, и тем переход из нарастания в убывание произойдёт раньше. При этом характер звучания в нашем восприятии формируют главным образом, гармоники с наибольшей скоростью нарастания.
***
Резонансы несущей конструкции гитары, как и многих других струнных инструментов, создают в струне девиации частот и различные для разных гармоник параметры нарастания и убывания амплитуды. Когда-то первые музыкальные синтезаторы, а затем и компьютеры не могли моделировать эти факторы, и звучание получалось лишь отдалённо похожим на звучание реальных инструментов. И лишь появление высокопроизводительных компьютеров и соответствующего софта позволило моделировать звучания практически неотличимо от оригинала.
Однако, несмотря на большую значимость для формирования звучания, совокупность этих факторов не удостоилась специального термина. Я предлагаю назвать это динамической эквализацией. Соответственно, эквализацию, получаемую, например, с помощью электронных формирователей тембра, называть статичной эквализацией.
И теперь мы можем ответить на целый ряд вопросов.
Первое: почему ничего не дал эксперимент с пропусканием звука через деревянную мембрану?
Всё просто: широко распространено мнение, что проходя через древесину, звук непостижимым, почти волшебным образом улучшается-насыщается-обогащается, а это не так. Создаётся некоторая статичная эквализация, не более того. Без динамической эквализации класс звучания остаётся прежним, плохой звук остаётся плохим.
Второе: влияет ли несущая конструкция электрогитары на звучание?
Однозначно, ДА. И в акустических и в электрических струнных инструментах звучание формируется в струне, и качество и характер этого звучания в огромной мере зависит от качества динамической эквализации, создаваемой резонансами несущей конструкции. При этом индукционные датчики так же создают динамическую эквализацию своими резонансами.
Третий вопрос более изощрённый: влияет ли гриф гитары на звучание?
Влияет, причём у электрогитары-боди резонанс грифа самый сильный. Статичное упругое сопротивление грифа ниже, чем у корпуса, соответственно, при практически одинаковой добротности, резонанс сильнее. В акустической гитаре резонанс грифа заметно слабее резонанса деки, но он так же создаёт динамическую эквализацию, которой может не только улучшать, но и портить звучание.
Четвёртый: можно ли статичной эквализацией исправить недостатки динамической?
В очень ограниченных пределах. Если динамическая эквализация некой гитары такова, что она звучит как консервная банка, с помощью статичной эквализации электронного эквалайзера вы сможете получить звучание другой консервной банки, и даже жестяного ведра, но никак не хорошей гитары.
Означает ли это, что статичная эквализация совсем бесполезна? Вовсе нет, наилучшее звучание получается благодаря грамотному сочетанию обоих видов эквализации.
***
Далеко не праздный вопрос: сколько резонансов нужно для хорошего звучания? Чем больше, тем лучше? Разумеется, это не так. Если частоты хотя бы двух резонансов при некоторой добротности сблизятся настолько, что уменьшится разница между минимумами и максимумами АЧХ в диапазоне этих резонансов, то оба они потеряют выразительность, что ухудшит звучание инструмента в целом. Схождение резонансов – очень распространенная ошибка, как плохих мастеров, так и неграмотных разработчиков в серийном производстве.
Желательно, чтобы диаграмма частота-упругое сопротивление состояла сплошь из наклонных линий.
Получается, увеличивая количество резонансов, мы должны повышать их добротность. И насколько же мы можем их повысить? До каких пределов?
Загвоздка в том, что детали несущей конструкции при игре совершают не только вынужденные колебания на частотах колебаний струн (почти), но и свободные на своих собственных частотах, воруя для этого энергию у струн. И чем выше добротность резонансов этих деталей, тем больше амплитуда и длительней сустейн их собственных колебаний.
При оптимальных значениях добротности эти колебания очень толково прикидываются реверберацией, но при значениях выше оптимальных образуют неприятный гул. Он тем более неприятен, что не вписывается ни в одну тональность, поскольку детали несущей настраиваются в четверть тона от хроматических ступеней.
Так мы попадаем в жёсткие рамки: низкая добротность резонансов приводит к невыразительному звучанию, а слишком высокая к гулу.
Для достижения хорошего звучания добротность резонансов несущей конструкции должна находиться в узких оптимальных пределах.
Поэтому не имеет смысла располагать резонансы ближе 9-ти полутонов, а чаще всего их располагают в интервалы в 11 или 13 полутонов. Не рекомендуется располагать в 12 полутонов (чистую октаву). 6-7 резонансов при правильной расстановке по частотам и оптимальных значениях добротности дают отличное профессиональное звучание, дальнейшее наращивание количества резонансов заметного улучшения звучания не даёт.
1.5. Декремент затухания как удельное свойство материала
А есть у материала свойство, влияющее на добротность резонанса физического тела? У металлических струн, особенно у дискантов, сустейн заметно длительней, чем у нейлоновых. У металлофона он в разы длительней, чем у ксилофона. Несомненно, материал обладает как минимум, одним свойством, определяющим декремент затухания тела. И называется оно так же: логарифмический декремент затухания. Учёные мужи не удосужились придумать для этого свойства собственное название. Поэтому приходится различать ЛДЗ как характеристику тела или конструкции, и ЛДЗ как удельное свойство материала.
В общих чертах, ЛДЗ как свойство материала – это ЛДЗ некого стандартного образца из этого материала при некоторых стандартных условиях. И это очень важная характеристика материала для музыкальных инструментов. В первую очередь, оно оказывает сильное влияние на добротность резонансов физических тел.
Как мы помним, для хорошего звучания добротность резонансных тел должна находиться в некоторых оптимальных пределах. Соответственно, эти тела, проще говоря, детали инструментов очень желательно изготавливать из материалов с оптимальными показателями по ЛЗД.
Да, друзья, пригодность материала в качестве резонансного определяется не принадлежностью к древесинам, не способом просушки, не фактурой, не ценой, не плотностью, не страной произрастания, а в первую очередь показателем логарифмического декремента затухания.
Остаётся неясным, как нейлоновые струны умудряются сохранять строй, ведь декремент нейлона даже выше, причём намного, чем у древесины. Почему же нейлоновые струны не подвергаются сильным девиациям? Чтобы с этим разобраться, нужно ознакомиться с таким явлением, как
1.6. Механическое напряжение
Про электрическое напряжение нам рассказывали в школе, а про механическое (обозначается строчной греческой буквой сигма),

забыли рассказать. А оно гораздо проще для понимания.
Если вы сожмете рукой обычный кистевой эспандер, почувствуете силу, стремящуюся распрямить эспандер, и чем дольше будете его удерживать, тем лучше будете её чувствовать. Когда же вы его отпустите, он примет обычную свою форму.
При сжатии в нем возникло то самое механическое напряжение, а потом снялось.
Когда вы натягивание струну на гитаре, так явственно возникающее в ней напряжение не чувствуете, а оно возникает, и нарастает. И если вы перетянете струну, она лопнет. Напряжение превысит предел прочности, и разрешится в разрыв струны.
Величина механического напряжения выражается как сила, делённая на площадь, к которой она приложена. Для струны совсем просто: сила натяжения на площадь поперечного сечения керна.
Оно-то и понижает декремент затухания материала, и повышает добротность струны. Теперь нам понятно, почему карбоновые струны дают больше сустейна и обертонов, чем нейлоновые, а металлические больше, чем карбоновые. Сечение струны обратно пропорционально плотности материала, следовательно, напряжение ей прямо пропорционально.
Вот так струны из материала с высоким декрементом затухания обретают приемлемую добротность. Но всё же приходится слышать жалобы гитаристов-классиков на фальшь ля-большого на 6-й струне. На 5-й нет, а на 6-й есть! Дело в том, что 5-я и 6-я струны навиваются на одинаковый керн, чуть ли не с одной бобины, а 6-я обычно делается на меньшую силу натяжения. Соответственно, у неё ниже добротность, и она подвергается девиации от резонанса задней деки.
Вы могли заметить, что с ростом напряжения повышается собственная частота тела, в данном случае струны, но при этом ещё и понижается декремент затухания. И в нейлоновых струнах он достигает вполне приемлемых величин.
Напряжение в струне повышает не только добротность, но и склонность к образованию обертонов. До некоторого уровня оно улучшает звучание, однако при чрезмерно высоких значениях звук становится надсадным, неприятным.
Усилие натяжения струн передаётся и несущей конструкции, так же создавая в ней напряжение, и повышая добротность её резонансов. Особенно это заметно на передних деках акустических инструментов. И если добротность деки ниже оптимального значения, её можно повысить, создав дополнительные напряжения при помощи пружин. Пружина сгибается так же, как выгибаются обечайки, и приклеивается к деке внатяг. Так же небольшое напряжение создают некоторые лакокрасочные материалы, особенно нитроцеллюлозные.




