Теорема зонтика, или Искусство правильно смотреть на мир через призму математики

000
ОтложитьЧитал
LE THEOREME DU PARAPLUIE
Où l’art d’observer le monde dans le bon sens
Mickaël LAUNAY (Illustrations by Chloé Bouachour) © Flammarion, Paris, 2019
© Сысоева И., перевод на русский язык, 2022
© Оформление. ООО «Издательство «Эксмо», 2022

Введение
В 1980 году преподаватели из института математических исследований университета Гренобля предложили группе детей решить следующую загадку:
В лодке 26 овец и 10 коз; сколько лет капитану?
Странный вопрос. Какое отношение возраст капитана имеет к количеству овец и коз? Из почти двухсот опрошенных в возрасте от семи до восьми лет 75 % респондентов ответили без каких-либо сомнений. Многие просто сложили представленные числа и получили 36. Но, когда детям в возрасте от девяти до десяти лет предложили ту же загадку, большинство из них начали протестовать или даже отказались отвечать. Только 20 % ответили безоговорочно. За два года их критический настрой обострился. Эти дети стали проницательнее и начали сомневаться в смысле того, что они делают.
В их возрасте, должен признаться, я получал особое удовольствие от загадок-ловушек. Таких, которые заставляют мозг кипеть и которые, по сути, скорее шутки, чем математические задачки. Одна из моих любимых звучит так:
Оркестр из 50 музыкантов исполняет Симфонию № 9 Бетховена за 70 минут. За какое время оркестр из 100 музыкантов сыграет ту же симфонию?
Конечно, продолжительность симфонии не зависит от количества музыкантов, 70 минут так и останутся 70 минутами. Мне очень нравилась еще и эта загадка: что тяжелее: килограмм ваты или килограмм железа? Конечно, ни то, ни другое, поскольку они весят одинаково – килограмм.
Чего я не знал, так это того, что укрощение смысла вещей может привести гораздо дальше, чем я себе представлял. Чем дальше я продвигался, тем больше замечал тонкости в значении слов и пробелы в моем понимании мира. Конечно, взрослые уже не попадаются в те же ловушки, что и дети. Но было бы неверно полагать, что мы защищены от других заблуждений, подстерегающих нас. Наша интуиция может нас обмануть, а факты оказаться ложными. В свои 35 лет я могу сказать, что с самой начальной школы в моей жизни не было и года, чтобы я не осознавал, что ошибаюсь в том, что, как мне казалось, хорошо знаю.
Если мы хотим понять мир и окружающую нас действительность, то рискуем сбиться с толку. В глубине души великие ученые нашей истории мало чем отличались от детей, которые отказались назвать возраст капитана. Ученые сомневались в том, что у них перед глазами, и стремились увидеть больше. Они восставали против установленного порядка. Наука – замечательная почва для сомнений, а математика – один из самых мощных инструментов.
Заниматься математикой – как заглянуть за кулисы мира. Украдкой понаблюдать за гигантскими винтиками, которые вращают нашу Вселенную. Зрелище ослепительное, но и разрушительное. Реальность бросает вызов нашим чувствам и интуиции. Все оказывается не тем, чем нам представляется. Действительность переворачивает наши убеждения с ног на голову, а самые, казалось бы, очевидные вещи, сметает с доски. Самые безобидные детали способны скрывать великие тайны, а детские загадки иногда могут оказаться намного глубже.
Вот еще одна:
Если четыре курицы откладывают четыре яйца за четыре дня, то сколько яиц откладывают восемь куриц за восемь дней?
Я дам вам время на размышления, мы еще к ней вернемся. О чем я никогда и подумать не мог, так это о том, что эта загадка, которую я впервые услышал в десять лет, поможет мне понять самую известную формулу всех времен.
Поэтому, если вы согласитесь ненадолго со мной остаться, я предложу вам отправиться в путешествие. Нам могут повстречаться некоторые трудности, ведь нельзя изменить свое мышление по щелчку пальцев. На нашем пути попадутся сомнения, которые придется преодолеть, и появятся мысли, которые придется оставить созревать. Но не сдавайтесь – потраченные усилия будут вознаграждены тысячекратно, когда вас наконец осенит. На следующей странице начинается наше путешествие по математике, в котором мы откроем некоторые из самых красивых скрытых механизмов нашего мира. Поднимите на мгновение ваши глаза и оглядитесь: возможно, после нашего знакомства вы перестанете воспринимать мир, ваш мир, таким образом.
Часть I. Закон супермаркетов
Закон Бенфорда
Математические приключения иногда встречаются в самых безобидных местах.
Давайте начнем наше путешествие в супермаркете на углу, всего в шаге от вашего дома. В нем вы обычно делаете покупки – неважно, гигантский это торговый центр или деревенский мини-маркет; главное, чтобы там были самые разные товары первой необходимости, которые мы покупаем каждый день.
Обычный магазин. Вы бывали здесь уже сотни, может, даже тысячи раз. Ряды полок, проходы, ровный ритм считывания штрихкодов на кассах и клиенты, которые бродят вокруг, машинально хватая то бутылку молока, то консервную банку. Но сегодня мы ничего не покупаем. Мы наблюдаем.
Здесь спрятан один из самых интригующих математических самородков. Он всегда был тут – прямо у вас перед носом. И он даже не скрывается, вы видите его прямо сейчас. Небольшая аномалия. Пустяковая деталь, которая не привлекает внимания, тем не менее может вызвать подозрение у опытных наблюдателей. Достаньте блокнот или смартфон, нам он понадобится для заметок, и давайте начнем наше расследование.
Посмотрите на цены, выстроившиеся в ряд на полках. €2,30… €1,08… €12,49… €3,53… все эти числа кажутся совершенно случайными, если их быстро читать одно за другим. €1,81… €22,90… €0,64… цены варьируется от нескольких центов до нескольких десятков евро. Но мы не будем заострять внимание на деталях. Забудьте о запятых и сотых долях.
На каждом ценнике смотрите только на первую цифру, самую важную – она дает нам первое, приблизительное представление о цене. (Такие цифры в математике называют «значащими»).
Вот 530-граммовая банка консервированной брюссельской капусты за €1,54. Отметьте в вашем блокноте 1. Чуть дальше дезодорант, действующий 24 часа, за €3,53. Отметьте 3. 250 грамммов камамбера за €1,81. Еще одна 1 в вашем блокноте. Сковорода с антипригарным покрытием за €45,90 – здесь мы перевалили за десятку, но, несмотря ни на что, сосредоточиваемся только на первой цифре. Отмечаем 4. Пакет жареного арахиса за €0,74. В этот раз первая значащая цифра – 7.
Так, несколько минут блуждая по магазину, мы набрали цифры. 1 3 1 4 7 9 2 2 1 7 9 8 1 1 3 1 1 1 8 1 1 2 1 2 1 1 9 1 4 7 1 6 1 5 9 2 2 1 3 2 2 2 1 2 2 6…
Но отмеченные вами цифры вызывают смутное сомнение. Вам не кажется, что в этой череде что-то не так? Некий дисбаланс. Она преимущественно состоит из 1 и 2, перемежаясь то тут, то там 3, 4, 5, 6, 7, 8 и 9. Как будто мы, сами того не осознавая, обращали наше внимание на самые низкие цены. Так не пойдет.
Так что давайте поступим как добросовестные статистики. Оставим в стороне наши предубеждения и выберем систематический метод. Мы случайным образом укажем на несколько полок и выпишем значимые цифры со всех товаров без исключения. Да, это трудоемкая задача, но мы должны разобраться с ней до конца.
Через час страницы вашего блокнота покрыты рядами цифр. Пришло время подвести итоги. После подсчета вердикт не подлежит обжалованию, и тенденция подтвердилась. Вы перечислили цены на более чем тысячу товаров, и почти треть из них начинается с 1! Чуть больше четверти начинается с 2, и чем больше цифра, тем реже она встречается.
После компиляции мы пришли к следующим результатам[1].
В этот раз мы не можем сослаться на случайность или предвзятый выбор товаров. У нас есть доказательства, а потому надо признать факт: первые цифры цен в супермаркете распределены неравномерно. Преобладают – со значительным отрывом – небольшие цифры.
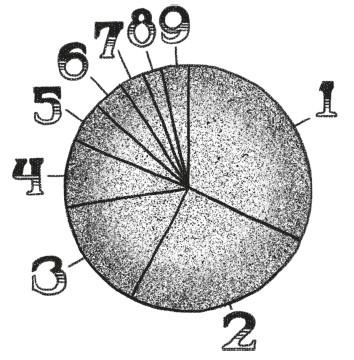
Откуда этот дисбаланс? Вот вопрос, который я хотел бы вам задать. Какому закону супермаркетов, торговли или экономики подчиняются эти ценники, чтобы дать такое странное, такое неравномерное распределение первых цифр? Разве математика не должна относиться ко всем цифрам[2] одинаково – без предвзятости, без предпочтений, без фаворитов? И все же факты налицо и категорически утверждают обратное: в супермаркете у математики есть любимчики – цифры 1 и 2.
Мы провели наблюдение. Мы установили закономерность. Теперь нам остается только подумать над ней, проанализировать и разобраться. У нас есть факты, и мы должны провести расследование и сделать свои выводы.
В марте 1938 года американский инженер и физик Фрэнк Бенфорд опубликовал статью «Закон аномальных чисел» (The Law of Anomalous Numbers), в которой он проанализировал числовые данные, полученные из более чем двадцати тысяч источников различного происхождения. В его таблицах можно найти список длин рек из разных частей земного шара, население разных городов США, атомные массы известных элементов, числа, случайно наблюдаемые в газетах, или математические константы. И по всем этим данным Бенфорд делает тот же вывод, что и мы: первые цифры распределены неравномерно. Около 30 % проанализированных чисел начинаются с 1, 18 % – с 2, и чем больше цифра, тем реже она встречается; так, только 5 % чисел начинаются с 9.
Бенфорду не пришла в голову идея проверить свою статистику в магазине. Но согласитесь: его результаты удивительно похожи на наши. Конечно, есть некоторые различия в процентах, но в общих чертах совпадение поразительно.
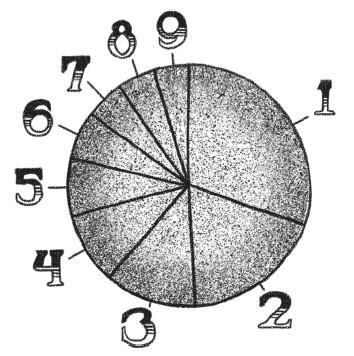
Исследование Бенфорда показало, что собранные нами данные – далеко не единичный пример. Они характерны не только для супермаркетов, но вписываются в гораздо более широкую тенденцию. После 1938 года такое же распределение наблюдалось многими учеными во множестве необычных и разнообразных ситуаций.
Например, в демографии. Население 62 из 203 стран на планете Земля – или 30,5 % – записывается числом, которое начинается с цифры 1. Взять, к примеру, самую густонаселенную: Китай с населением 1,4 млрд человек. К этим 62 странам также относится Мексика с населением 122 млн человек, Сенегал с населением 13 млн или архипелаг Тувалу с населением 10 800. При этом лишь в 14 странах (6,9 %) запись числа населения начинается с цифры 9.
Вам предпочтительнее астрономия? Из восьми планет, вращающихся вокруг Солнца, у четырех запись длины экваториального диаметра[3] начинается с цифры 1. У Юпитера – 142 984 км, у Сатурна – 120 536, у Земли – 12 756, у Венеры – 12 104. Диаметр самого Солнца составляет 1 392 000 км. И если выборка из девяти небесных тел недостаточно полна, чтобы вас убедить, добавьте сюда же карликовые планеты, спутники, астероиды, а также кометы, и вы все равно придете к тому же выводу: превалирует цифра 1.
Как только мы начинаем обращать на это внимание, примеры сыплются дождем. Возьмите любой набор чисел в любом контексте, проанализируйте первые цифры, и увидите: закон Бенфорда работает. Этот статистический закон совсем не исключительный, он, похоже, совершенно естественный и повсеместный. И, как ни парадоксально, равномерного[4] распределения цифр, которое могло бы показаться нам более интуитивно-вероятным, на практике просто не существует.
Здесь речь идет уже не о любопытном свойстве цен в супермаркетах. То, что мы обнаружили, – это настоящий закон, который регулирует не только многие области человеческой деятельности, но и саму природу. Понять этот закон – значит понять нечто фундаментальное об устройстве нашего мира.
Его влияние настолько велико, что мы подчиняемся ему, даже не осознавая этого. Люди, которые устанавливают цены в магазинах, не договариваются друг с другом и едва ли слышали о Фрэнке Бенфорде. И все же, неосознанно, словно ими манипулирует неподвластная им сила, они подчиняются его закону. Как и население стран, длины рек и диаметры планет.
В 1938 году Фрэнк Бенфорд назвал это распределение «законом аномальных чисел». Тем не менее этот закон настолько распространен, что такое название кажется неуместным. Аномальность субъективна и существует только в умах людей, которые ей поражаются. Природа, напротив, кажется, находит этот закон универсальным. Закон аномален только до тех пор, пока мы его не поймем. И мы намерены его понять.
Но в каком направлении двигаться? Как направить наши мысли, чтобы приоткрыть завесу тайны и понять аномалии?[5]
Закон Бенфорда несложно понять, но его объяснение не уложить в несколько строк. Математика, которая скрывается за ним, проста, но глубока. Это не загадка, решение которой неожиданно приходит в голову, и мы восклицаем: «Ах! Вот, в чем дело, я понял!» Нам придется поменять наше понимание природы чисел и сам подход к счету. Если закон Бенфорда не кажется нам очевидным, то это потому, что мы неправильно думаем. Нам придется научиться по-другому смотреть на то, что нам кажется таким знакомым. Нам придется снова ставить под сомнения свои суждения.
Из экскурсии по миру, который только что нам открыл Фрэнк Бенфорд, мы вернемся другими. Его закон изменит вас. И когда вы его поймете, вы будете думать совсем иначе.
Мультипликативное мышление
Повседневность часто намекает, что мы плохо управляемся с числами. Что с нами – или с ними – что-то не так.
У меня есть небольшая история на эту тему.
Несколько лет назад на вечеринке, которую мы с друзьями посвятили играм, кому-то пришла в голову идея устроить научную викторину. Мы разбились на две команды и отвечали на вопросы из разных сфер: от математики и геологии до биологии и информатики. На каждый вопрос команда должна была дать приблизительный ответ в численном выражении, и та, чей ответ был ближе всего к верному, зарабатывала очко. Правило казалось довольно простым и ясным. И все же после нескольких раундов вопрос из области астрономии вызвал неожиданный спор.
Нас спросили, каково расстояние между Землей и Луной.
В нашей команде никто не знал точного ответа, но, поразмыслив, мы ответили, что оно составляет 800 000 км. В команде противника переговоры оказались куда более напряженными, но в конце концов они объявили свой ответ: 10 км!
Очевидно, в этой команде в астрономии разбирались еще хуже, чем в нашей. Высочайшая вершина Земли, гора Эверест, достигает в высоту почти 9 км. Если бы Луна находилась всего в 10 км от Земли, чтобы коснуться нашего спутника, достаточно было бы подняться на гору. Абсурдный ответ. Еще одно очко, казалось мне, у нас в кармане.
Тем не менее правильный ответ нас озадачил. Луна на самом деле находится на расстоянии 384 000 км от Земли. Таким образом, простое вычитание показало нам, что мы ошиблись на 416 000 км, в то время как команда противника ошиблась только на 383 990 км.
Я моргнул и посчитал еще раз. Ошибки не было. Признаться, я даже нацарапал небольшую схему на бумажной салфетке, чтобы окончательно убедиться.
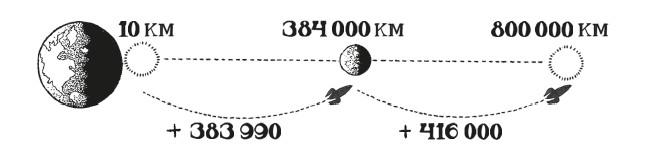
Сомнений не было: их ответ был ближе к правильному, чем наш. Они победили. Несколько минут я пересчитывал и прокручивал расчет в голове, но ничего не поделаешь. Математика была категорична.
Но все же, вам не кажется, что эта ситуация несправедлива? Да, возможно я выгляжу, как человек, который не умеет проигрывать, но вы не думаете, что, несмотря на результат, наш ответ был более разумным, более продуманным и, в некотором смысле, менее неправильным, чем у другой команды?
Но почему в таком случае математика говорит об обратном? Почему расчеты показывают, что почти абсурдный ответ ближе к истине?
Или стоит задать вопрос немного по-другому: правильно ли мы понимаем математику, которой пользуемся? Математика не ошибается, но люди, которым она служит, иногда могут использовать ее ненадлежащим образом.
Если немного подумать, то можно представить множество подобных ситуаций. Рост кошки в среднем составляет 25 см, а лабрадора – 60 см. Некоторые бактерии достигают в длину одну тысячную миллиметра. Таким образом, можно утверждать, что по размеру кошка ближе к бактериям, чем к лабрадору. Разница в росте между кошкой и бактериями составляет около 25 см, а между кошкой и собакой – 35 см.

Но это заключение, к которому нас подводят числа, снова противоречит нашему естественному восприятию реальности. Кошка и собака принадлежат к одному миру. Они могут играть вместе или, по крайней мере, взаимодействовать. Они видят друг друга, чувствуют друг друга, они знают, что оба существуют. Но кошка, если, конечно, она не изучала науку, понятия не имеет о существовании бактерий. Они не являются частью ее мира, они настолько малы, что их невозможно ни увидеть, ни даже вообразить.
Можно привести еще несколько похожих примеров, которые кажутся интуитивно нелогичными, но все же математически точными. Температура на поверхности Солнца ближе к 5 °C, чем к 15 000 °C. Население Парижа ближе к населению деревни с 12 жителями, чем к населению Нью-Йорка. Если вы взвесите планету Марс, то обнаружите, что ее масса ближе к массе мячика для пинг-понга, чем к массе Земли.
Как и в случае с законом Бенфорда, эти ситуации ставят нас в логический тупик только потому, что мы думаем неверно. Потому что мы используем математический инструментарий, который плохо понимаем, в контексте, в котором он неуместен.
Как же тогда воплотить эти интуитивные размышления в математике? Ответ можно найти в тонком понятии порядка величины.
Сама идея простая, но невероятно мощная. Думать посредством порядка величины – значит думать с помощью умножения, а не сложения.

Если вы хотите сравнить числа 2 и 10, вы можете сделать это двумя разными способами. Путем сложения: сколько нужно добавить к 2, чтобы получить 10? В таком случае ответ 8. Или путем умножения: на сколько нужно умножить 2, чтобы получить 10? Тогда ответ равен 5. В первом случае разница между двумя числами получается путем вычитания: 10 ÷ 2 = 8. Во втором – деления: 10 ч 2 = 5.
Сказать, что два числа имеют одинаковый порядок величины, значит сказать, что они близки с точки зрения умножения.
Несмотря на то, что на первый взгляд эта идея кажется довольно странной, любой, кто начинает мыслить мультипликативно, то есть посредством умножения, быстро понимает, насколько этот подход лучше соответствует нашей интуиции.
Вернемся к нашей научной викторине. Вот как я мог бы отстоять нашу победу в игре, если бы тогда мыслил здраво. Луна находится на расстоянии 384 000 километров от Земли, а наша команда ответила, что на расстоянии 800 000 км, то есть примерно в два раза дальше. Если мы поделим числа, то окажется, что наш ответ был в 2,08 раза больше верного. Наши противники ответили, что расстояние составляет 10 км, то есть в 38 400 раз меньше правильного ответа! С этой точки зрения мы действительно победили. Более того, этот результат гораздо лучше соответствует нашему интуитивному восприятию мира.
Такой подход сработает и со всеми остальными примерами. Если считать мультипликативно, то размер кошки ближе к размеру собаки, чем к размеру бактерии, масса Марса ближе к массе Земли, чем к массе мячика для пинг-понга, население Парижа ближе к населению Нью-Йорка, чем к населению маленькой деревни, и так далее.

Когда мы сравниваем два числа, независимо от контекста, в котором происходит это сравнение, чаще всего мы интуитивно прибегаем к мультипликативному мышлению. Если в вашем супермаркете товар стоимостью 200 евро подорожает на 8 евро, то, несомненно, это подорожание вас расстроит, но гораздо меньше, чем если бы на те же 8 евро подорожал товар стоимостью 2 евро. В таком случае цена увеличивается до 10 евро, то есть в 5 раз! Расстроиться – это мягко сказано. И это при том, что номинально цены выросли на одну и ту же величину.
Таким подходом к сравнению мы обязаны не только работе интеллекта. Это не уникальное свойство мышления, он естественен для нас и моделирует большинство наших взаимодействий с миром. Наше чувственное восприятие окружающего мира тоже мультипликативно.
Если я завяжу вам глаза и вложу в одну руку предмет весом 10 г, а в другую – весом 20 г, вы сразу же поймете, какой из них тяжелее. Но различить «на ощупь» предметы весом 10 кг и 10 кг и 10 г куда сложнее. Однако разница в парах одинаковая: 10 г. Или, точнее, разница одинаковая с точки зрения сложения, или аддитивности, потому что с точки зрения умножения она вопиющая: 20 г в два раза тяжелее, чем 10 г. Во втором же случае разница между двумя массами составляет всего 0,1 %.
То же можно сказать и про наше зрение. Вы когда-нибудь пробовали включить свет средь бела дня? Если солнце уже заливает комнату, это почти ничего не меняет. Яркость кажется одинаковой независимо от того, светит лампочка или нет. Но если вы включите свет ночью, то ясно увидите, как он освещает самые темные уголки, которые мгновение назад терялись в полумраке.
Тем не менее днем лампочка излучает не меньше света, чем ночью. То есть с точки зрения сложения яркость одинакова в обеих ситуациях. Но наши глаза воспринимают эту яркость иначе – относительно, то есть мультипликативно. При дневном свете яркость лампочки незначительна по сравнению с яркостью Солнца. Ночью же все меняется – она правит бал.
Это справедливо и для остальных органов чувств: осязания, зрения, вкуса, слуха, обоняния. Подумайте хотя бы о том, как вы воспринимаете течение времени, преодоленное расстояние, и, что более субъективно, интенсивность эмоций, которые испытываете. Все эти чувства гораздо проще поддаются пониманию, когда вы начинаете думать о них мультипликативно, а не аддитивно.
- Теорема зонтика, или Искусство правильно смотреть на мир через призму математики



